Western University's Free Appropriate Sustainability Technology (FAST) Research GroupWanted! Students to make a distributed future with solar-powered open-source 3-D printing and recycling. Contact Dr. Joshua Pearce - Apply here
Home · Projects & Publications · Methods · Literature reviews · People · Sponsors · News · Twitter/X · YouTube · LinkedIn · For kids!
Read more...
This page is a literature review.Feel free to edit this page and add sources and summaries.Read more...

Motivation[edit | edit source]

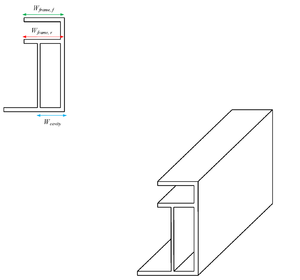
Sustainable development of renewable energy sources requires decreasing photovoltaic (PV) energy generation prices in all aspects.[1][2] A critical step towards this goal is to reduce the installation costs of PV power plants.[3][4] Considering conventional PV modules,[5][6] which currently use commercially available aluminum frames shown in Fig. 1, a noticeable portion of installation costs will be allocated to the connection of PV module to racking system using clamps or other methods[7].[8][9]

Furthermore, one of the essential applications of PV technology is to empower people having no access to the electricity grid, such as developing countries' villages[10] or agricultural fields users.[11][12] For these people, it is vital if they can set up their PV power plant own their own, and if they face problems in this regard, PV technology cannot be considered their priority.[13][14] Connecting the aluminum frames illustrated in Fig.1 directly to the racking system could have some complexity, especially for ordinary people if they are going to do so;[15] therefore, specialists would be needed to connect the PV module to the racking. All of the reasons mentioned above can increase the costs of PV power plant establishment, consequently decreasing people's desire to invest in PV technology.

Fig.1. Conventional PV frames currently using in the industry

Literature Review[edit | edit source]

Early contributions, Investigation of impact of solar cells thickness on their stability[edit | edit source]

In the literature, there have been some research articles addressing PV frames performance under a mechanical loads. In the real world conditions, some situations such as snow accumulation imposes severe loading threatening integrity of PV modules by breaking glass cover and solar cells.[16] Also considerable defects created under mechanical loads such as micro-cracks should be considered.[17][18] Seminal contribution were made by Wohlgemuth et al.[19] in 2008 when they have developed a test procedure to evaluate cracked cells in PV modules. Chen et al.[20] in the same year used Abaqus software for finite element method (FEM) analysis (FEA) to measure residual stress in the silicon solar cells. They found that reducing wafer thickness causes an increase in residual stress and bow. Pingel et al.[21] in 2009 found similar results and evaluated the mechanical stability of solar cells considering the cell thickness, cell interconnection technology, and cell supplier using some industry accepted standards such as analyzing IV curves and electroluminescence images. They found that decreasing solar cells thickness could reduce the stability of solar cells significantly. Following the previous study, Burn et al.[22] proposed a method for analyzing the fracture of crystalline silicon wafers during the handling and transportation process by analyzing the wafer's overall stress state by measuring the deformation of wafer and doing non-linear finite element method (FEM) analysis. They showed that according with the linear elastic fracture mechanics hypothesis, solar cell wafer breakage stress during the handling and transpiration process is proportional to the inverse of the square root of the crack length.

Effect of mechanical loads in creating cracks and consequently reducing PV modules power output[edit | edit source]

In lining with previously discussed papers, In 2010, Popovich et al.[17] point out that reducing the silicon thickness without respecting its strength could result into significant surface and edge defects such as micro-cracks, grain boundaries and surface roughness during the handling and transpiration. They tried to provide some information regarding bending strength of solar cells with the aid of four-point bending test. As a result, they mentioned that metallization morphology, crystallinity of silicon solar cells, and eutectic layer could contribute noticeable differences in fracture strength of them. Also, they discovered that aluminum paste effects the strength of solar cells. In 2011, Kajari-Schroder et al.[23][24] deeply discussed the role of cracks in PV power output, they note that these cracks, created by mechanical loads could effect the PV output. They proposed a statistical analysis to evaluate the crack formation in 27 crystalline silicon (c-Si) PV modules under a mechanical load defined at IEC 61215 10.16. IEC 61215 is a standard test monitoring reliability of PV modules under 2400 Pa and subsequently 5400 Pa uniform pressure on the module surface. They resulted that 50 percent of the damaged cells are fractured parallel to the busbars, a crack direction with a large potential influence on the PV module's power output.These cracks may separate a huge cell area, resulting in a significant decrease in the PV's power output. Köntges et al.[18] discuss further power loss problems caused by micro-cracks. The performed some experiments to assess how how micro-cracks would affect PV module's power and used computer simulations to classify the cracks in the wafer not harming metallization of the Si cells. They[18] demonstrated that the immediate influence of micro-cracks on Si PV module's power is negligible, however the presence of micro-cracks may be significant for the module's performance following artificial ageing. They[18] discussed two viable techniques for preventing power loss caused by micro-cracks: the primary strategy is to prevent cell rupture.The second technique may involve employing a more flexible cell metallization that prevents electrical separation of cell sections in the event that the silicon is damaged. In investigating cracks created in solar cells, Sander et al.[25] study fulfilled the outcomes of above-discussed researches, in which they developed a systematic approach analyzing the effect of load direction on the cracks direction. They showed that loading parallel to the busbars is more critical than loading perpendicular to the busbars, particularly for multi c-Si cells, and that cracks arise primarily at the solder or lamination process-induced cracks.

Reliability of PV modules under dynamic mechanical loads[edit | edit source]

Assmus et al.[26] study in 2011 was a step forward in analyzing PV modules under dynamic mechanical loads such as wind imposing vibrations on the module. They performed some outdoor measurements monitoring deflection of PV modules under dynamic wind load to correlate wind velocity and deflections, and compared the numerical calculation to FEM modeling. They reported that the real world oscillations were smaller than static load caused by IEC 61215 2400 Pa mechanical load. Similarly, Bosco et al.[27] note that dynamic mechanical load could result in fatigue and failing of interconnect ribbons in PV modules made of copper, where considerable number of ribbons might be stretched beyond 2%. In another study, Bosco et al.[28] conducted FEM simulations to evaluate fatigue in flat PV solder joints in the different climate zones. They[28] showed that solder fatigue damage's rate is dependent on three climatic variables: mean daily maximum cell temperature, mean daily maximum cell temperature change, and the number of temperature reversals throughout a characteristic temperature. They[28] finally presented a empirical formula in this regard based on the results of seven studied cities.

Reliability of PV modules under static mechanical loads[edit | edit source]

FEM considering all important component of PV modules such as cells, polymer layers and frame was used by Dietrich et al.[29] in 2012. They calculated failure chance of each solar cell by Weibull distribution function.Their outcomes demonstrate a relationship between the frame section's stiffness and the type of mounting, where if the size of the load varies, the recommended frame and mounting selection may also change. In addition, in their analysis, the stiffness of the encapsulant were observed to correlate with the fundamental mechanical behaviour of the module laminate. They found that at high stiffness values, a sandwich behaviour predominates, while at low stiffness values, a laminate behaviour with shear deformation predominates. More FEM analyses in this context were done by Lee et al.[16] in 2013, when they evaluated silicon (Si) PV modules under mechanical load test mentioned in IEC 61215. They conducted FEA to investigate the stress on PV module. Their results show that solar cells at the center of PV module experiences the highest tensile stress, and cells at the edges of module meet compressive stress, therefore they are free from fracture problem. However, they conclude that since silicon is really a brittle material that exhibits a high scattering of fracture stress, and as other experiments[30] suggest that silicon fails under the same conditions, their FEA simulation may not be completely reliable. In addition, they noted that fracture failure is inevitable for non-tempered glass considering their tensile strength.

Effect of boundary conditions and and the mounting system on the deflections and stresses within PV modules[edit | edit source]

Industry makes a variety of PV module mounting solutions, usually including a frame of metallic beams with a second frame of beams positioned perpendicular to the first beam layer. The most used mounting system in PV industry is comprised a base aluminum structure including prefilled bars which are screwed to the aluminum S shaped clamps, holding the top face of module frame profile so that it brings the frame's lower side into frictional contact with the profiled bar as stated in Fig.2.[31] Although currently using PV mounting systems provide reliable safety for PV panels installations, they are complex to setup. The mounting system defines the boundary conditions for FEA. Schicker et al.[31] mentioned that FEM result can be significantly impacted by the boundary conditions. They[31] employed various simplified estimations in FEM on the real clamping of PV modules to simulate the deformation of the module and, consequently, the value of stress-strain in the solar cells and compared the results to some experimental findings. They[31] found that especially weak modules, such as thin frame and thin glass plate, exhibit a remarkable dependence of cell stresses on the FE model's boundary conditions and small variations of stress may result in massively higher values of stressors. Finally the authors[31] concluded that three primary contributing factors could be important in stiffening a PV module and reducing its deflections as well as stresses, which are glass thickness, the frame stiffness, and the laminate embedment depth in the frame.Deflections and stresses of the module are highly dependent on the stiffness behaviour of ethylene vinyl acetate (EVA).

Fig.2. Clamps for connecting conventional PV frames to racking


In 2016, Beinert et al. study[32] accomplished the Schicker et al.[31] study by comparing the clamping of framed and unframed standard glass-backsheet PV modules under 2400 Pa and 5400 Pa using FEA, respectively. They considered the thermal stress from lamination process in their analysis as well. They reported that frame-less PV laminate (Maximum tensile stress of 443 MPa) experienced 147 mm higher displacement compared to framed PV (Maximum tensile stress of 268 MPa) of modules under 5400 Pa. Furthermore, unframed PV (Maximum tensile stress of 218 MPa) showed consequently 54 mm higher deflections compared to framed PV (Maximum tensile stress of 142MPa) under uniform pressure of 2400 Pa. The aforementioned results are inline with findings of.[23][24][33] Their final results[32] indicate the critical role of frames in PV modules, which diminishes the tensile stresses in solar cells compared to unframed laminates. Beinert and Masolin[34] presented an innovative mounting solution in 2020 using FEM, which improves the mechanical stability PV modules.Their novel mounting solution (Coolback® system) is the combination passive cooling and mounting structure that replaces the backsheet and frame and it covers the entire rear side of the module. They[34] found that a module utilizing a rear side mounting with cooling fins drastically decrease module deflection, resulting in negligible solar cell breakage probability under all loads. Especially under higher loads, when the framed module has a high probability of solar cell fracture, the cooling fins' greater mechanical stability helps to reduce cell fracture. However, the note that the PV laminate inside a conventional frame has a lower maximum tensile stress because of local tensile stress around the clamp.

Recent contributions[edit | edit source]

In 2020, Beinert et al.[35] evaluated the impact of solar cell and module dimensions under the load of 2400Pa on the thermomechanical stress within PV module based on FEM. They changed number (from 60 to 140 cells) and the format (from full cells down to quarter cells) of solar cells within PV module. Their simulation covered lamination process, mechanical loads and thermal cycling for two type of glass-foil and glass-glass modules.Their provided results demonstrate that Increase in cell size has the most significant impact on stress.For glass–glass modules, the stress and accompanying failure probability are low for all variants simulated due to positioning of solar cells in the neutral zone, which reduces stress to negligible levels. Lamination could generate compressive stress in solar cells, which does not cause cell breaks but can cause de-lamination and ribbon fatigue. In the same year Hartley et al.[36] performed quasi-static three-dimensional FEM simulations on the aluminum framed c-Si PV modules and compared them with experiential data. They performed parametric analysis by Latin hypercube sampling along with sensitivity analysis using linear correlation coefficients as well as variance-based sensitivity indices to identify crucial parameters affecting module deformation. Their results showed that module deflection is strongly associated with glass thickness, elastic modulus as well as edge tape and adhesive material properties indicating that optimizing these materials could result in increasing module stiffness comparable to conventional structural factors, such as glass thickness. Additionally, they found that despite being crucial for establishing nominal modeled-to-experimental deflection agreement, module assembly factors such as friction coefficients and preloads did not seem to be significantly linked with expected module deflection. Their study proves the suitability of FEM simulations for accurately forecasting the mechanical behaviour of solar modules.

A recent comprehensive study were done by Tummalieh et al.[37] finding the most appropriate dimension of conventional PV frame profile illustrated in Fig.1 using FEA, Cell-to-module (CTM) and life cycle assessments which are 18 mm for both front and rear frame widths and cavity width of 12 mm. The aforementioned dimensions improve the overall performance of the PV modules and aids in achieving a balance among technical performance, cost, and environmental effects. Also, their FEA[37] showed that even little variations in the width of the frame has a large effect on the stress within the solar cells. Their optimized frame has 2.6% less deflections, and can save 30 g aluminum and 0.8 kg CO2-eq/kWP, consequently decreasing the total module cost by 0.1% compared to reference dimensions (16mm front frame width, 20 mm rear frame width and 8.5mm cavity width). However, it slightly reduces PV module power by 0.4 WP

Literature Gaps and Novelty[edit | edit source]

References[edit | edit source]

  1. ↑ Yaqoot, Mohammed; Diwan, Parag; Kandpal, Tara C (2016). "Review of barriers to the dissemination of decentralized renewable energy systems". Renewable and Sustainable Energy Reviews 58: 477–490. ISSN 1364-0321.
  2. ↑ Strupeit, Lars; Palm, Alvar (2016). "Overcoming barriers to renewable energy diffusion: business models for customer-sited solar photovoltaics in Japan, Germany and the United States". Journal of Cleaner Production 123: 124–136. ISSN 0959-6526.
  3. ↑ Morris, Jesse; Calhoun, Koben; Goodman, Joseph; Seif, Daniel (2014). "Reducing solar PV soft costs: A focus on installation labor". 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC). IEEE. pp. 3356–3361. ISBN 1-4799-4398-3.
  4. ↑ Yilmaz, Saban; Ozcalik, Hasan Riza; Kesler, Selami; Dincer, Furkan; Yelmen, Bekir (2015). "The analysis of different PV power systems for the determination of optimal PV panels and system installation—A case study in Kahramanmaras, Turkey". Renewable and sustainable energy reviews 52: 1015–1024. ISSN 1364-0321.
  5. ↑ Mesquita, D. D. B., Silva, J. L. D. S., Moreira, H. S., Kitayama, M., & Villalva, M. G. (2019, September). A review and analysis of technologies applied in PV modules. In 2019 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America) (pp. 1-6). IEEE.
  6. ↑ Powell, D. M., Winkler, M. T., Choi, H. J., Simmons, C. B., Needleman, D. B., & Buonassisi, T. (2012). Crystalline silicon photovoltaics: a cost analysis framework for determining technology pathways to reach baseload electricity costs. Energy & Environmental Science, 5(3), 5874-5883.
  7. ↑ Arefeen, Shamsul; Dallas, Tim (2021). "Low-cost racking for solar photovoltaic systems with renewable tensegrity structures". Solar Energy 224: 798–807. ISSN 0038-092X.
  8. ↑ Franz, Jacob; Morse, Stephen; Pearce, Joshua M (2022). "Low-cost pole and wire photovoltaic racking". Energy for Sustainable Development 68: 501–511. ISSN 0973-0826.
  9. ↑ Vandewetering, Nicholas; Hayibo, Koami S.; Pearce, Joshua M. (2022). "Impacts of Location on Designs and Economics of DIY Low-Cost Fixed-Tilt Open Source Wood Solar Photovoltaic Racking". Designs 6 (3). doi:10.3390/designs6030041. ISSN 2411-9660.
  10. ↑ Akinsipe, Olusola Charles; Moya, Diego; Kaparaju, Prasad (2021). "Design and economic analysis of off-grid solar PV system in Jos-Nigeria". Journal of Cleaner Production 287: 125055. ISSN 0959-6526.
  11. ↑ Qoaider, Louy; Steinbrecht, Dieter (2010). "Photovoltaic systems: A cost competitive option to supply energy to off-grid agricultural communities in arid regions". Applied Energy 87 (2): 427–435. ISSN 0306-2619.
  12. ↑ Jones, MA; Odeh, I; Haddad, M; Mohammad, AH; Quinn, JC (2016). "Economic analysis of photovoltaic (PV) powered water pumping and desalination without energy storage for agriculture". Desalination 387: 35–45. ISSN 0011-9164.
  13. ↑ Rai, Varun; Reeves, D Cale; Margolis, Robert (2016). "Overcoming barriers and uncertainties in the adoption of residential solar PV". Renewable Energy 89: 498–505. ISSN 0960-1481.
  14. ↑ Reindl, Katharina; Palm, Jenny (2021). "Installing PV: Barriers and enablers experienced by non-residential property owners". Renewable and Sustainable Energy Reviews 141: 110829. ISSN 1364-0321.
  15. ↑ Palm, Jenny (2018). "Household installation of solar panels–Motives and barriers in a 10-year perspective". Energy Policy 113: 1–8. ISSN 0301-4215.
  16. ↑ 16.0 16.1 Lee, Yixian; Tay, Andrew A. O. (2013-01-01). "Stress Analysis of Silicon Wafer-Based Photovoltaic Modules Under IEC 61215 Mechanical Load Test". Energy Procedia. PV Asia Pacific Conference 2012 33: 265–271. doi:10.1016/j.egypro.2013.05.067. ISSN 1876-6102. Retrieved 2022-05-24.
  17. ↑ 17.0 17.1 Popovich, V. A.; Yunus, A.; Janssen, M.; Richardson, I. M.; Bennett, I. J. (2011-01-01). "Effect of silicon solar cell processing parameters and crystallinity on mechanical strength". Solar Energy Materials and Solar Cells. 19th International Photovoltaic Science and Engineering Conference and Exhibition (PVSEC-19) Jeju, Korea, 9-13 November 2009 95 (1): 97–100. doi:10.1016/j.solmat.2010.04.038. ISSN 0927-0248. Retrieved 2022-05-25.
  18. ↑ 18.0 18.1 18.2 18.3 Köntges, M.; Kunze, I.; Kajari-Schröder, S.; Breitenmoser, X.; Bjørneklett, B. (2011-04-01). "The risk of power loss in crystalline silicon based photovoltaic modules due to micro-cracks". Solar Energy Materials and Solar Cells 95 (4): 1131–1137. doi:10.1016/j.solmat.2010.10.034. ISSN 0927-0248. Retrieved 2022-05-25.
  19. ↑ Wohlgemuth, John H; Cunningham, Daniel W; Placer, Neil V; Kelly, George J; Nguyen, Andy M (2008). "The effect of cell thickness on module reliability". 2008 33rd IEEE Photovoltaic Specialists Conference. IEEE. pp. 1–4. ISBN 1-4244-1640-X.
  20. ↑ Chen, Chih-Hung; Lin, Fu-Ming; Hu, Hsuan-Teh; Yeh, Fang-Yao (2008). "Residual stress and bow analysis for silicon solar cell induced by soldering". International symposium on solar cell technologies. pp. 4–6.
  21. ↑ Pingel, S; Zemen, Y; Frank, O; Geipel, T; Berghold, J (2009). "Mechanical stability of solar cells within solar panels". Proc. of 24th EUPVSEC: 3459–3464.
  22. ↑ Brun, Xavier F.; Melkote, Shreyes N. (2009-08-01). "Analysis of stresses and breakage of crystalline silicon wafers during handling and transport". Solar Energy Materials and Solar Cells 93 (8): 1238–1247. doi:10.1016/j.solmat.2009.01.016. ISSN 0927-0248. Retrieved 2022-05-25.
  23. ↑ 23.0 23.1 Kajari-Schröder, Sarah; Kunze, Iris; Eitner, Ulrich; Köntges, Marc (2011-11-01). "Spatial and orientational distribution of cracks in crystalline photovoltaic modules generated by mechanical load tests". Solar Energy Materials and Solar Cells 95 (11): 3054–3059. doi:10.1016/j.solmat.2011.06.032. ISSN 0927-0248. Retrieved 2022-05-25.
  24. ↑ 24.0 24.1 Kajari-Schršder, S.; Kunze, I.; Kšntges, M. (2012-01-01). "Criticality of Cracks in PV Modules". Energy Procedia. Proceedings of the 2nd International Conference on Crystalline Silicon Photovoltaics SiliconPV 2012 27: 658–663. doi:10.1016/j.egypro.2012.07.125. ISSN 1876-6102. Retrieved 2022-05-25.
  25. ↑ Sander, Martin; Dietrich, Sascha; Pander, Matthias; Ebert, Matthias; Bagdahn, Jörg (2013-04-01). "Systematic investigation of cracks in encapsulated solar cells after mechanical loading". Solar Energy Materials and Solar Cells 111: 82–89. doi:10.1016/j.solmat.2012.12.031. ISSN 0927-0248. Retrieved 2022-05-25.
  26. ↑ Assmus, Marcus; Jack, Steffen; Weiss, Karl-Anders; Koehl, Michael (2011). "Measurement and simulation of vibrations of PV-modules induced by dynamic mechanical loads". Progress in Photovoltaics: Research and Applications 19 (6): 688–694. doi:10.1002/pip.1087. ISSN 1099-159X. Retrieved 2022-05-25.
  27. ↑ Bosco, Nick; Silverman, Timothy J; Wohlgemuth, John; Kurtz, Sarah; Inoue, Masanao; Sakurai, Keiichiro; Shioda, Tsuyoshi; Zenkoh, Hirofumi et al. (2013). "Evaluation of Dynamic Mechanical Loading as an accelerated test method for ribbon fatigue". 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC). IEEE. pp. 3173–3178. ISBN 1-4799-3299-X.
  28. ↑ 28.0 28.1 28.2 Bosco, Nick; Silverman, Timothy J; Kurtz, Sarah (2016). "Climate specific thermomechanical fatigue of flat plate photovoltaic module solder joints". Microelectronics Reliability 62: 124–129. ISSN 0026-2714.
  29. ↑ Dietrich, Sascha; Sander, Martin; Pander, Matthias; Ebert, Matthias (2012-10-16). "Interdependency of mechanical failure rate of encapsulated solar cells and module design parameters". Reliability of Photovoltaic Cells, Modules, Components, and Systems V. 8472. Reliability of Photovoltaic Cells, Modules, Components, and Systems V. SPIE. pp. 123–131. doi:10.1117/12.929289. Retrieved 2022-05-25.
  30. ↑ Popovich, V. A.; Yunus, A.; Janssen, M.; Richardson, I. M.; Bennett, I. J. (2011-01-01). "Effect of silicon solar cell processing parameters and crystallinity on mechanical strength". Solar Energy Materials and Solar Cells. 19th International Photovoltaic Science and Engineering Conference and Exhibition (PVSEC-19) Jeju, Korea, 9-13 November 2009 95 (1): 97–100. doi:10.1016/j.solmat.2010.04.038. ISSN 0927-0248. Retrieved 2022-05-25.
  31. ↑ 31.0 31.1 31.2 31.3 31.4 31.5 Schicker, Johannes; Hirschl, Christina; R.Leidl (2014-07-01). "Effect of PV Module Frame Boundaries on Stresses in Solar Cells". Journal of Energy Challanges and Mechanics 1. doi:10.13140/2.1.3374.1441.
  32. ↑ 32.0 32.1 Beinert, Andreas; Ebert, Matthieu; Eitner, Ulrich; Aktaa, Jarir (2016-06-20). Influence of Photovoltaic Module Mounting Systems on the Thermo-Mechanical Stresses in Solar Cells by FEM Modelling.
  33. ↑ Eitner, Ulrich; Kajari-Schröder, Sarah; Köntges, Marc; Altenbach, Holm (2011). "Thermal stress and strain of solar cells in photovoltaic modules". Shell-like Structures. Springer. pp. 453–468.
  34. ↑ 34.0 34.1 Beinert, Andreas; Masolin, Alex (2020-09-07). Enhancing PV Module Thermomechanical Performance and Reliability by an Innovative Mounting Solution.
  35. ↑ Beinert, Andreas J.; Romer, Pascal; Heinrich, Martin; Mittag, Max; Aktaa, Jarir; Neuhaus, D. Holger (2020-01). "The Effect of Cell and Module Dimensions on Thermomechanical Stress in PV Modules". IEEE Journal of Photovoltaics 10 (1): 70–77. doi:10.1109/JPHOTOV.2019.2949875. ISSN 2156-3403.
  36. ↑ Hartley, James Y.; Owen-Bellini, Michael; Truman, Thomas; Maes, Ashley; Elce, Edmund; Ward, Allan; Khraishi, Tariq; Roberts, Scott A. (2020-05). "Effects of Photovoltaic Module Materials and Design on Module Deformation Under Load". IEEE Journal of Photovoltaics 10 (3): 838–843. doi:10.1109/JPHOTOV.2020.2971139. ISSN 2156-3403.
  37. ↑ 37.0 37.1 Tummalieh, Ammar; Beinert, Andreas J.; Reichel, Christian; Mittag, Max; Neuhaus, Holger. "Holistic design improvement of the PV module frame: Mechanical, optoelectrical, cost, and life cycle analysis". Progress in Photovoltaics: Research and Applications n/a (n/a). doi:10.1002/pip.3533. ISSN 1099-159X. Retrieved 2022-05-24.
FA info icon.svg Angle down icon.svg Page data
Authors Seyyed Ali Sadat
License CC-BY-SA-4.0
Language English (en)
Related 0 subpages, 1 pages link here
Impact 315 page views
Created May 24, 2022 by Seyyed Ali Sadat
Modified June 9, 2023 by StandardWikitext bot
Cite as Seyyed Ali Sadat (2022–2023). "Open-source PV frame design:FAST literature review". Appropedia. Retrieved April 28, 2024.
API queries basic, semantic, html, files, more
Retrieved from "https://www.appropedia.org/w/index.php?title=Open-source_PV_frame_design:FAST_literature_review&oldid=743307"
Cookies help us deliver our services. By using our services, you agree to our use of cookies.