
Simple and easy to produce, temporary housing platform to to aid in living conditions after a natural disaster
What's Going On[edit | edit source]


Survivors of natural disasters, such as the 2004 tsunami in the Indian Ocean and the 2009 earthquakes in Haiti, are left homeless. As a result victims will construct shanty camps, neighborhoods, and towns to fit the need of shelter.[1] These camps are crowded and typically very unclean.[2] Residents live at ground level with the camp's sewage, garbage and debris from the disaster.[3] These living conditions cause the spread of disease and can contaminate living conditions for an entire family.[2][4] Further natural forces such are wind and rain can batter and demolish these make shift encampments, causing more deaths, disease and hardship.[5]
What We are Trying to Address
The concept behind the relief platform is simple, to give people a lift. By raising people 20 centimeter off the ground the majority of the the waste, debris and sewage will not longer contaminate a persons living area.[2] A solid foundation will also give a structure a chance to withstand subsequent natural forces, and not get blown or washed away.[5]
Limitations[edit | edit source]
There are many solution to temporary housing after natural disasters. One of the most successful in the aftermath of the Haitian earthquakes was the ShelterBox.[6] A ten person tent accompanied with sleeping bags, small tools, and other survival supplies. Many other conceptual design for relief efforts have been put forward all addressing the direct need for shelter.[7] The existing problem with the majority of these current solutions is that they do not address the need of a foundation. Most are still tent structures that have no base, and therefore are susceptible to rain and wind.[8][9] The Relief Platform is not a direct solution. Its goal to to give survivors the necessary foundation to build a structure, by offering the occupants a dry safe place to live.
After Life[edit | edit source]
In the spirit of William McDonough's 'Cradle to Cradle', the Relief Platform can be reused in other applications. With normality returning to an area and low level construction starting the platform can become a more permanent footing for housing. The platform can also be recycled as raised decking or as an outdoor shower platform. If no other use for the platform can be found it can always be redeployed in other disaster zones or its materials can be separated and recycled.
The Product[edit | edit source]
Below is a conceptual design for the Relief Platform. NPS 2, SCH 40 piping is constructed into trusses. The trusses build the frame of the platform with, the "floor" constructed from wood. Below is a rendering of the relief platform.

A Bit of Engineering[edit | edit source]
Several key engineering aspects of the platform have to be reviewed. First, we have to look at the structural rigidity of the "floor". Making the assumptions that the beams used at 2"x4" wooden beams we can say that the Youngs Modulus of the wood is 12GPa. Next we use Equation 1 to determine the beams moment of inertia.
(1)[10]
From this we determine the moment of inertia to be . These are the material constant elected to be used in the platform. Modeling the floor boards as a double fixed beam, we set the maximum defection of the beams to be 1cm. With this information a short iterative process can be applied to find the optimum beam length to load. To do this the floor is modeled as a series of beam with fixed ends and a uniform applied load. From this model Equation 2 is derived to describe the deflection
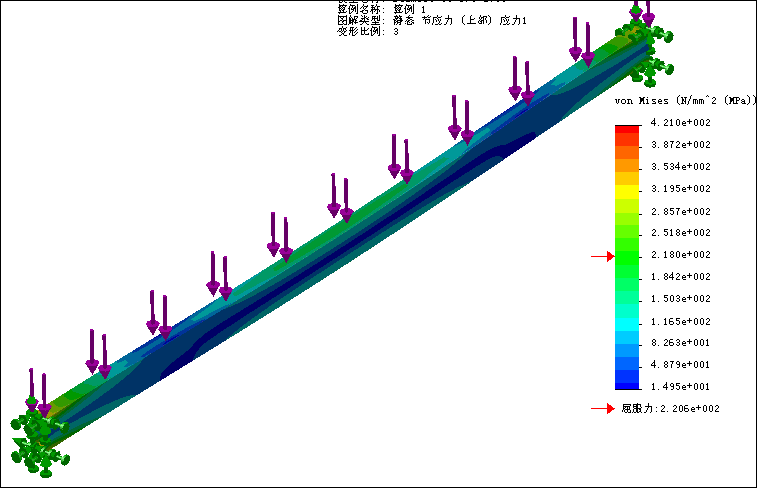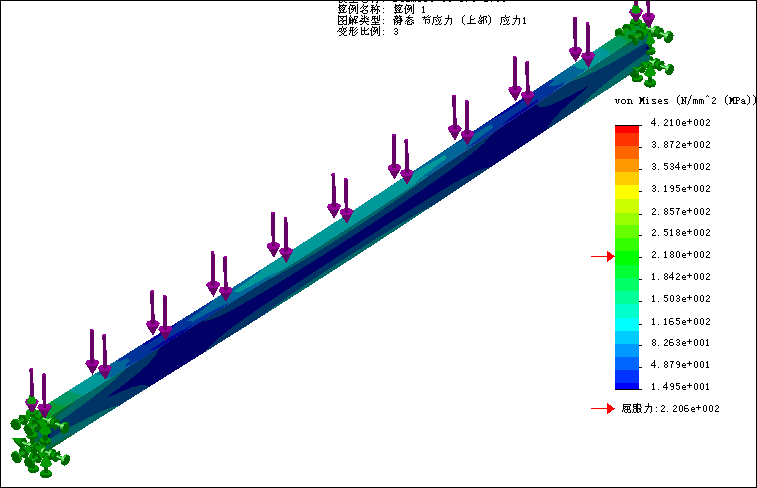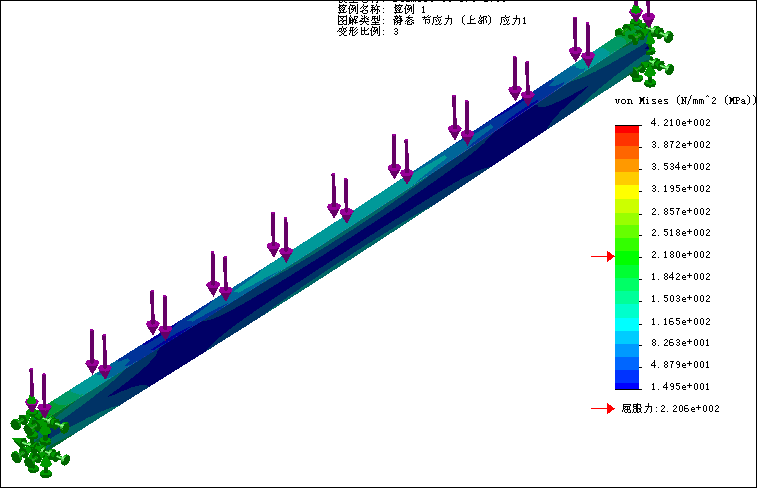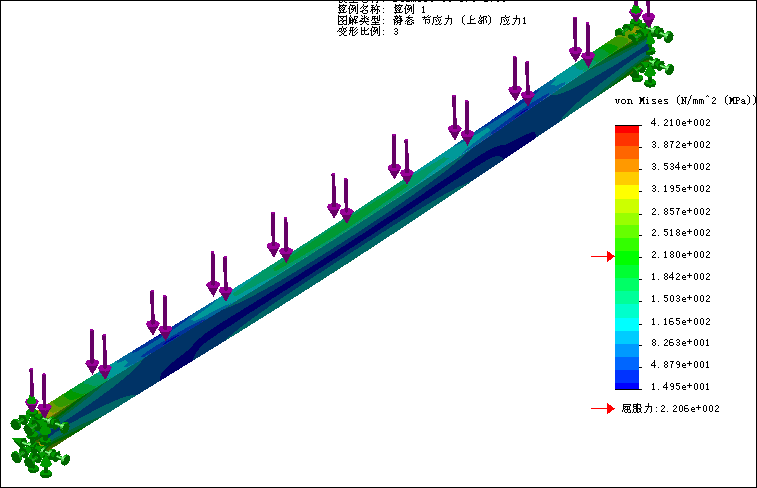
(2)[10]
Because the beam is redundant the moment M' must be solved from the boundary conditions. Once done the moment is found to be
(3)[10]
Substituting Equation 3 back into Equation 2 and solving for the length L we are left with
(4)[10]
We determine the ultimate strength of wood to be:
for tension[10]
for compression[10]
for shear[10]
to check that the load does not exceed any of these material limits Equations 5 and 6 are used to calculate the shear stress and normal stress respectively
(5)[10]
For this double fixed beam the shear is:
(5.1)[10]
With the area of the beam
(5.2)[10]
(6)[10]
By substituting Equation 1 and 3 in to the above formula the normal stress at any point 'y' can be found.
Using Equation 4 in a trial and error iteration we optimize the beams length. Using a spreadsheet the relative uniform loads and length are calculated
| Uniform Load {} [N/m] | Length {L} [m] | Uniform Weight {P} [kg/m] | Total Weight {W} [kg] |
|---|---|---|---|
| 100 | 4.76 | 10.2 | 48.5 |
| 200 | 4.00 | 20.4 | 81.5 |
| 300 | 3.61 | 30.6 | 110.5 |
| 400 | 3.36 | 40.8 | 137.1 |
| 500 | 3.18 | 51.0 | 162.1 |
| 600 | 3.04 | 61.2 | 185.8 |
| 700 | 2.92 | 71.4 | 208.6 |
| 800 | 2.83 | 81.5 | 230.6 |
| 900 | 2.75 | 91.7 | 251.9 |
| 1000 | 2.67 | 101.9 | 272.6 |
| 1100 | 2.61 | 112.1 | 292.8 |
From this iteration it is decided that a 2.75 meter beam holding roughly 250kg is suitable.
From Equations 5 and 6 it is determined that a 2.75 meter beam is to long and would exceed the woods ultimates strengths. Therefore the beam length is reduced to 2.0 meters and a second iteration using Equations 5 and 6 is done to determine ultimate load.
| Uniform Load {} [N/m] | Length {L} [m] | Uniform Weight {P} [kg/m] | Total Weight {W} [kg] | Moment {M'} [Nm} | Shear Force {V} [N] | Normal Stress {} [MPa] | Shear Stress {} [MPa] |
|---|---|---|---|---|---|---|---|
| 50 | 2.00 | 5.1 | 10.2 | 16.7 | 50.0 | 0.38 | 0.0097 |
| 60 | 2.00 | 6.1 | 12.2 | 20.0 | 60.0 | 0.46 | 0.0116 |
| 70 | 2.00 | 7.1 | 14.3 | 23.3 | 70.0 | 0.53 | 0.0136 |
| 80 | 2.00 | 8.2 | 16.3 | 26.7 | 80.0 | 0.61 | 0.0155 |
| 90 | 2.00 | 9.2 | 18.3 | 30.0 | 90.0 | 0.69 | 0.0174 |
| 100 | 2.00 | 10.2 | 20.4 | 33.3 | 100 | 0.76 | 0.0194 |
| 200 | 2.00 | 20.4 | 40.8 | 66.7 | 200 | 1.53 | 0.0388 |
| 300 | 2.00 | 30.6 | 61.2 | 100 | 300 | 2.29 | 0.0581 |
From both iterations a design length of 2 meters is chosen. This will allow for a reasonable living size () as well as a reasonable load limit per beam (). These design criteria assume that the average human will stand on at least 2 beams at once, dispersing the load, and will weigh approximately 75kg. This also give the floor a safety factor of 2
Assembly[edit | edit source]
The core of the platform is its truss frame. This frame give the platform strength and rigidity, as well as allowing it to be linked together and secured down.

Secured to the Relief Platform are the floor boards. In this case 2"x4" beams are used but other local materials can also been used in the floors construction

The platforms can be linked with 'U' brackets to build larger living spaces.


Pricing[edit | edit source]
The final cost of the platform is estimated at $300.
The steel piping costes are calculated from the total length of piping require. In this case it is estimated that the platform will use 12 meters of the schedule 40 piping. At a cost of 2.95 $/ft[11] the total piping cost is estimated at $118.
The same calculation applies to the wood. A total of 20 beam, each 2 meters long, are required. this give a total amount of wood at 40 meters. At a cost of 4.49 a meter this costs a total of $180.
Features[edit | edit source]
The Relief Platform is 2 by 2 meters giving the floor a safety factor of roughly 2. This allows for other less "structural" materials then woods to be used. The platform includes anchors at all corners so that tents, tarps and awnings can be secured and will not blow away in the wind. This also allows for the platform to be secured to other foundations or structures. These anchors also make stacking the platforms for transport easier. Interlocking pins allow for many platforms to be linked together.

References[edit | edit source]
- ↑ ["'Amnesty International': International Aid Orginization". Gerardo Ducos. livewire.amnesty.org. 15 March, 2010. [1]] Copyright Amnesty International. 2010]
- ↑ 2.0 2.1 2.2 ["'The Washington Post': International News Organization". Peter Slevin. www.washingtonpost.com. 03 Feb, 2010. [2]] Copyright The Washington Post. 2010]
- ↑ ["'The Christian Science Monitor': International News Orginization". Kathie Klarreich. www.csmonitor.com. 02 Feb, 2010. [3]] Copyright The Christian Science Monitor. 2010]
- ↑ ["'Wikipedia': Online Encyclopedia". www.wikipedia.com. 12 April, 2010. [4]] Copyright Wikipedia. 2010]
- ↑ 5.0 5.1 ["'The Red Cross': International Aid Organization". www.redcross.org. 22 March, 2010. [5]] Copyright The Red Cross. 2010]
- ↑ ["'ShelterBox': Emergency Relief Group". www.shelterbox.ca. 21 Jan, 2010. [6]] Copyright ShelterBox. 2010]
- ↑ ["'Wire': Technological Magazine". Jenna Wortham. www.wired.ca. 22 Oct, 2007. [7]] Copyright Wired. 2010]
- ↑ ["'Habitat for Humanity': International Aid Orginization". www.habitat.org. 2010. [8]] Copyright Habitat for Humanity. 2010]
- ↑ ["'The Christian Science Monitor': International News Orginization". Matthew Clark. www.csmonitor.com. 13 Jan, 2010. [9]] Copyright The Christian Science Monitor. 2010]
- ↑ 10.00 10.01 10.02 10.03 10.04 10.05 10.06 10.07 10.08 10.09 10.10 ["'Mechanicals of Materials': Engineering Textbook". R. C. Hibbeler. Seventh Edition. 2008. Copyright Pearson Education. 2008]
- ↑ ["'Global Technology and Engineering': Harware Supplier". 2010. Global Tech. 2010]
See also[edit | edit source]
Lightweight structural panels 3D print




![{\displaystyle L={\sqrt[{4}]{\frac {-384EIv}{\omega }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b639fbd084cbb8c1221c1a0721995b2c1864a0b9)











