The primary goal of this Appropriate Technology project is to consolidate existing information on solar cooking, as well as evaluate materials and design techniques utilized for the construction of widely used solar box cooker models.
Although hundreds of innovative solar cooker designs have been invented including the popular parabolic and panel cookers, the solar box cooker is given the widest consideration due to its widespread global usage, particularly in the developing world. See The solar cooking archive wiki for exhaustive details
- Most of the content from this page has been moved to solar cooker leaving mainly the design of the box solar cooker. To see the original content click here
Solar cooker[edit | edit source]
Several engineers and DIY enthusiasts have designed literally hundreds of different types of solar cookers; from simple designs like the solar bowling oven to more complicate ones like the parabolic basket and tin can solar cooker. This expansive variety of options makes it difficult to standardize and evaluate solar cookers, however some critical factors must be met for a design to be successful, some of which are listed below: Cost - must be cheap enough to be viable for implementation into rural areas.
- Convenience - can be built by readily available local materials in a short period of time, as well as being light-weight.SOL
- Safety - heated area must be well protected and no parts should be jutting out.
- Efficiency - how long will it take to cook the food?
- Wind resistance - must be sturdy enough to not be affected by light to moderate winds.
- Heating capacity - sufficient heating capacity based on it's use (water pasteurization vs. cooking food).
- Durability - repairs should be infrequent and easily performed.
- Simplicity of instructions.
The requirements for solar cooking are very simple. You must be able to place the solar cooker in a location that gets sun for several hours and be protected from strong wind. Solar cookers, obviously do not work at night or on very cloudy days. The sunlight is absorbed on dark surfaces that heat up. Food cooks best in dark, shallow, thin metal pots with dark, tight-fitting lids to hold in heat and moisture. To retain the heat created when the black pot absorbs the suns rays some form of transparent cover is needed. This can be as simple as a clear plastic bag or as complicated as evacuated multiple layers of glass. One method to speed the cooking process is to use reflectors to increase the concentration of sunlight on your collector.
Solar box cooker[edit | edit source]

Although hundreds of innovative solar cooker designs have been invented, the solar box cooker is given the widest consideration due to its widespread global usage, particularly in the developing world.
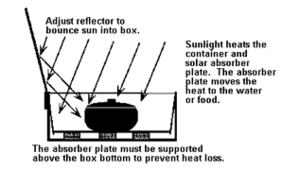
A solar box cooker is basically a large box with a glass lid that will function as an oven. However, the heat losses over a larger surface area will partially offset the additional gain through having a greater heat collecting surface. What is usually done to compensate for this is that a glazed surface cover and reflectors are used to increase the apparent collector area. These reflectors can be made from a variety of materials and their primary purpose is to reflect sunlight through the glazing material and into the cooking space inside of the box.
The box cooker consists of some type of heat trapping enclosure, which usually takes the form of a box made of insulating material with one face of the box fitted with a transparent medium, such as glass or plastic. This enables the cooker to utilize the greenhouse effect and incident solar radiation cooks the food within the box. The insulating material allows cooking temperatures to reach similar levels on cold and windy days as on hot days, as well as having an added benefit of blocking any leakages that could potentially seep through and damage the cooker. A dark cooking pot is recommended for cooking as it absorbs the maximum amount of heat and allows for higher cooking temperatures.[3]
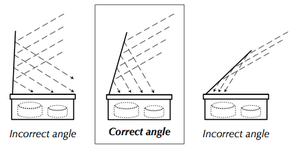
A good rule of thumb that indicates when the sun is high enough in the sky to allow for efficient cooking is when the length of one's shadow on the ground is shorter than that individual's height.
Developmental need[edit | edit source]
Cooking in developing countries is customarily done on open fires using biomass such as firewood, charcoal, and kerosene. This process inevitably leads to excessive deforestation in these rural regions as well as considerably increase CO2 emissions. Individuals in these developing regions also suffer from respiratory infections due to significant smoke inhalation.
About 5 million children in the developing world die each year from respiratory ailments and a further 5 million are estimated to die from diseases associated with contaminated drinking water.[5] These figures can hope to be partially reduced using solar cooking technology.
Solar cookers work on the basic principle of sunlight being converted to thermal energy that is retained and used for outdoor cooking purposes, and have the most positive impact in sunny, fuel-scarce regions of the world. An optimistic estimate states that solar cooking could cause a potential reduction of fuelwood use by 36% which corresponds to approximately 246 million metric tons of wood each year, thus resulting in a net greenhouse gas offset of nearly 140 million metric tons per year.[6]
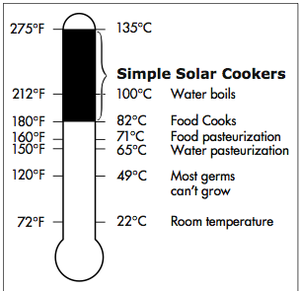
Figure 1 shows what processes occur over a temperature distribution of 135 degrees Celsius.
Regional considerations[edit source]
Approximately 600,000 solar cookers are being used in the Andes, Tibet, Nepal, Mongolia and parts of China and an estimated 1.5 million around the entire world, although this figure is preliminary and has yet to be confirmed of it's accuracy.[7][8] However, the biggest recent success story has been in villages in India.
Solar cooking may be suitable for a region if:
- Mostly-sunny days throughout several months of the year.
- Outdoor space available that remains sunlit for several hours and sheltered from high winds.
- Local cooking fuels are expensive or difficult to obtain.
Due to the abundance of sunlight in Asia, Africa, and Australia, these regions can greatly benefit from the use of solar cookers as illustrated in Figure 2.
As well as sunnier climates benefiting more from solar cooking technologies, locations with less windier conditions will be able to utilize solar cookers much more efficiently. In windier areas, it may be more suitable to introduce heavier solar cookers, however this could lead to higher cost implications and longer cooking times if thicker bases are constructed, as additional raw material would be required. Another crude but cheaper option would be to place large stones or bricks around the cooker to help stabilize it in the wind.
Efficiency analysis[edit | edit source]
Here is an efficiency analysis of solar cookers based on the 1st Law of Thermodynamics and the 2nd Law of Thermodynamics, explaining also how to calculate the cooking power of any device.
Required tools and materials[edit | edit source]
A sturdy solar box cooker can be built from cheap and common materials in a matter of a few hours without the use of additional tools. To increase durability, outer, non-reflective surfaces can be painted, oiled or waxed to help protect from moisture. The surface that faces the cooking pot should be reflective or black.
| Core materials | Substitute Materials |
|---|---|
| Aluminum foil | Metal or sheet metal |
| Black paint | Wax or oil |
| 2 large cardboard boxes | Woven baskets, bricks, wood (last option) |
| Heat resistant plastic sheets | Nylon bags, Polyester bags, Glass |
| Water-based polyvinyl acetate glues (diluted with water) | Wheat or rice flower paste, acacia gum, casein glue * |
* Avoid using tape petroleum and rubber-based glues for inner cooking surfaces, as the inner box should be able to withstand high temperatures without releasing any fumes.
Required skills and knowledge[edit | edit source]
There are no prerequisite skills or knowledge that are required to follow instructions on how to build a solar cooker. A few hours of basic training is needed to help educate masses living in rural areas on the basic construction and maintenance of solar cookers, after which they should be able to use them without any hassles, assuming that this training will include how to deal with all types of repairs pertaining to that particular solar cooker model.
Sample Dimensions[edit | edit source]
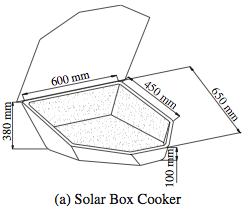
Building a Solar Box Cooker[edit | edit source]
Several successful solar box cooker designs have been established, accompanied with simple building instructions as well as tips and tricks. Some are listed below:
- Minimum Solar Box Cooker.[10]
- Solar Box Cooker.[11]
- Collapsible Solar Box Cooker.[12]
- Inclined Solar Box Cooker.[13]
- Tracking Box Cooker.[14]
- The Tire Cooker.[15]
Cost estimates[edit | edit source]
Approximately 2,400 square centimeters of scrap aluminum plate will make one 20 cm x 27.5 cm x 5.5 cm pan, with cover. The material cost is less than $0.30 per pan.[16]
This can be used as a reference to construct your own solar cooker with the aluminum plates available locally. The size of the cooker will be dependent on the size of the pan, and the overall unit size is subject to what is most economical in your particular geographic region.
| Materials | Estimated Rates ($) | Cost for project ($) |
|---|---|---|
| Aluminum sheet | $1->100,833 cm3[17] | $0.30 |
| Black paint | $16.14/L[18] | (~300 ml requirement) ~ $4.84 |
| 2 large cardboard boxes | $1.4/m2[19] | ~$1.47 |
| Glass | $10.76/m2[20] | (~0.27m2 requirement) -> ~ $2.91 |
| Acacia gum | ~ $3.50/kg[21] | (~0.25kg requirement) ~ $0.875 |
| TOTAL COST = | $10.39/unit |
These prices were determined through mainstream North American stores such as Home Depot, and size estimations based on the dimensions in Figure 5. The assumption is that the total cost of $10.39 will be significantly lower in rural locations due to less mark-up of the prices as well as easier accessibility to low-grade materials in these areas.
Future development focus[edit | edit source]
In order to progress with this technology, more resilient efforts must be made to educate the masses in rural areas and measures should be put into place to continue motivating these individuals to use these solar cookers on a regular basis.
Wind-resistant models would prove to be of great benefit in making solar cookers viable in more regions around the world, where powerful winds across open areas pose a current challenge to this technology.
Mass production of some the solar box cooker models aforementioned can result in further cost reductions if pre-made products are introduced to areas of need, instead of training camps being set up to teach these individuals how to make their own.
Related organizations[edit | edit source]
Several Non-Government Organizations (NGO's) and private organizations have taken it upon themselves to promote the benefits of solar cooking in developing rural areas, from creating DIY designs to setting up training camps to educate villagers on how to build and cook with these devices. Several of these organizations have successful cooker designs already posted online, and others are in various stages of design. Some of these groups are listed below:
- Solar Cookers World Network. http://solarcooking.wikia.com
- Solar Cookers International. http://www.solarcookers.org/
- Kyoto Twist Solar Cooking Society. http://web.archive.org/web/20200928080713/http://kyototwist.org/
- Gadhia Solar Energy Systems Pvt. Ltd. http://solarcooking.wikia.com/wiki/Gadhia_Solar_Energy_Systems
- Solar Energy International. http://www.solarenergy.org/
- Centre for Rural Technology. http://web.archive.org/web/20050207224602/http://www.panasia.org.sg:80/nepalnet/crt/crthome.htm
- The Central American Solar Energy Project. http://solaroven.org/
- SUN OVENS International, Inc. http://www.sunoven.com
- Lazola-Initiative. http://www.lazola.de
References[edit | edit source]
- ↑ The Solar Cooking Archive, "Evaluating Solar Cookers", solarcooking.org/Evaluating-Solar-Cookers.doc, Accessed April 8, 2010
- ↑ Solar Cookers International, "How to make a solar cooker", http://images3.wikia.nocookie.net/ cb20090108164302/solarcooking/images/5/57/CooKit plans detailed.pdf, Accessed April 6, 2010
- ↑ Wikipedia, "Solar cooker", http://en.wikipedia.org/wiki/Solar_cooker, Accessed April 3, 2010
- ↑ Solar Cookers International, "How to make a solar cooker", http://images3.wikia.nocookie.net/__cb20090108164302/solarcooking/images/5/57/CooKit_plans_detailed.pdf, Accessed April 6, 2010
- ↑ The Solar Cooking Archive, "Evaluating Solar Cookers", solarcooking.org/Evaluating-Solar-Cookers.doc, Accessed April 8, 2010
- ↑ The Solar Cooking Archive, "Evaluating Solar Cookers", solarcooking.org/Evaluating-Solar-Cookers.doc, Accessed April 8, 2010
- ↑ The Solar Cooking Archive, "Evaluating Solar Cookers", solarcooking.org/Evaluating-Solar-Cookers.doc, Accessed April 8, 2010
- ↑ Deutsche Welle, "Cooking with the power of the sun", http://www.dw-world.de/dw/article/0,,5205895,00.html, Accessed April 3, 2010
- ↑ Ozturk, H. "Second Law Analysis for Solar Cookers", http://www.informaworld.com/smpp/1138067100-85020668/content~db=all~content=a713635696, Accessed April 8, 2010
- ↑ The Solar Cooking Archive, "Minimum Solar Box Cooker", http://solarcooking.wikia.com/wiki/Minimum_Solar_Box_Cooker, Accessed April 8, 2010
- ↑ Solar Cookers International, "How to make a solar cooker", http://images3.wikia.nocookie.net/__cb20090108164302/solarcooking/images/5/57/CooKit_plans_detailed.pdf, Accessed April 6, 2010
- ↑ The Solar Cooking Archive, "The Collapsible Solar Box Cooker", http://solarcooking.org/plans/collapsible-box.htm, Accessed April 8, 2010
- ↑ The Solar Cooking Archive, "The Inclined Box-Type Solar Cooker – A New Design", hhttp://solarcooking.org/plans/inclined-box-cooker.htm, Accessed April 8, 2010
- ↑ The Solar Cooking Archive, "The Tracking Solar Cooker", http://solarcooking.org/plans/Cookerbo.pdf, Accessed April 8, 2010
- ↑ The Solar Cooking Archive, "The Tire Cooker", http://solarcooking.org/plans/tire_eng.htm, Accessed April 8, 2010
- ↑ The Solar Cooking Archive, "SunPan Overview", http://www.sungravity.com/sunpan_overview.html, Accessed April 4, 2010
- ↑ The Solar Cooking Archive, "SunPan Overview", http://www.sungravity.com/sunpan_overview.html, Accessed April 4, 2010
- ↑ Home Depot, "Painter's Touch Multi-Purpose Paint", http://www.homedepot.ca/webapp/wcs/stores/servlet/CatalogSearchResultView?D=980065&Ntt=980065&catalogId=10051&langId=-15&storeId=10051&Dx=mode+matchallpartial&Ntx=mode+matchall&recN=0&N=0&Ntk=P_PartNumber, Accessed April 8, 2010
- ↑ Shopping.com, "11" x 14" Corrugated Cardboard Sheets", http://www0.shopping.com/-cardboard+sheets, Accessed April 8, 2010
- ↑ GlassCages, "1/8 Plate Glass 3 mm Regular Plate Glass", http://www.glasscages.com/?sAction=ViewCat&lCatID=42, Accessed April 8, 2010
- ↑ Al-Mosawi. A, "Acacia gum supplementation of a low-protein diet in children with end-stage renal disease", http://www.springerlink.com/content/1rq1mafd2x233aa9/, Accessed April 8, 2010