
The objective of this project is to construct a device that aids the students of Zane Middle School in Eureka, California in the understanding of how civilizations moved water throughout the centuries. Through participating in the Engr205 Introduction to Design course at Cal Poly Humboldt and the University's partnership with Zane Middle School, a team referred to as The Amenders, shown in Figure 1, was born. By a process of trial and error, we have found that a model of an Archimedes Screw serves as a useful teaching aid. The Archimedes Screw instilled a curiosity among students that left them eager to learn more.
Background[edit | edit source]

Joan Crandell is a 6th grade teacher at Zane Middle School. Zane Middle School is a 6th-8th grade school located in Eureka, Ca. Zane focuses on STEAM education (Science, Technology, Engineering, Art, and Mathematics). Joan contracted with our team, The Amenders, to build a water transportation demonstration device for her 6th grade classroom.
Problem statement and criteria[edit | edit source]
The objective of this project was to build a device that demonstrates how water is transported between two target reservoirs. The Amenders designed an Archimedes Screw that moves water from a low reservoir to a higher reservoir located 3 feet above the ground. The design criteria given by the client, Joan Crandell, are listed in Table 1.
| Criteria | Weight | Constraints |
|---|---|---|
| Safety | 10 | Will not jeopardize safety of user(s). |
| Educational Value | 10 | Will provide students with a better understanding of how water is moved. |
| Ease of Use | 7 | Usable without prior understanding. |
| Durability | 9 | Will last for 5 years with reasonable care and maintenance. |
| Inspiration | 8 | Device usage promotes inquisitive interjections. |
| Aesthetics | 6 | Allows users to visually observe the process. |
| Setup Time | 5 | Set up time not to exceed 10 minutes. |
| Cost | 1 | Less than $400 total. |
Description of final project[edit | edit source]
The device being implemented is modeled after an Archimedes Screw. An Archimedes screw is a device used to transport water from a low elevation to a higher elevation. By using this model, students will be able to observe water ascending through the spiral tubes as they rotate the handle. The design consists of three main parts: the Archimedes Screw, the frame to support the screw, and two reservoirs for containing water.
-
Figure 2: Archimedes Screw Pump Final Design with Component Labels.
Costs[edit | edit source]
The following figure and tables address the materials used to build the Archimedes Screw Pump, associated costs, design time in hours, and estimated maintenance cost in hours in Figure 3, Table 2, and Table 3, respectively.
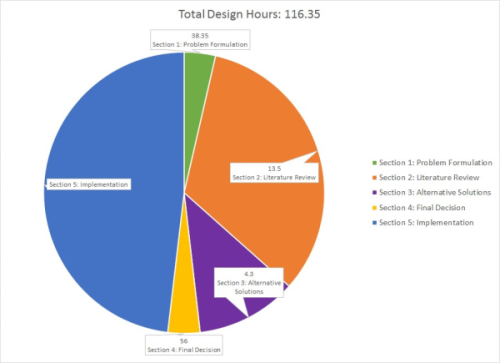
| Item | Amount | Price | Cost |
|---|---|---|---|
| 1/2" PVC Elbow | 2 | $0.49 | $0.98 |
| 2x6" Wood | 2 | Donated | $0 |
| 2x4" Wood | 2 | Donated | $0 |
| Screws | 4 | $0.23 | $0.92 |
| 1/2" X 2' PVC | 1 | $1.39 | $1.39 |
| 4" PVC cap | 1 | $3.99 | $3.99 |
| 2 oz. Gorilla Glue | 1 | $4.99 | $4.99 |
| Sand Paper | 1 | $1.49 | $1.49 |
| 5/8 ID X 7/8 OD Vinyl Tube | 17 | $1.29 | $21.93 |
| Spray Paint | 2 | $2.49 | $4.98 |
| PVC Reducer | 1 | $15.00 | $15.00 |
| Deck screws | 1 | $5.00 | $5.00 |
| PVC cement | 1 | $7.00 | $7.00 |
| Total | - | - | $67.67 |
| Action | Hours |
|---|---|
| Tighten Frame Hardware | 1.0 |
| Tighten Screw Hardware | 0.5 |
| Total Hours | 1.5 |
Testing Results[edit | edit source]
Two small scale models of the Archimedes Screws, shown in figure 4, were showcased at Zane Middle School's Galileo Day on April 3rd, 2015. The devices were a great success, and students and teachers alike lined up to use the Archimedes Screws. After using the device, students were eager to interject with questions about the Archimedes Screw. Upon the success at Galileo Day, a large-scale Archimedes Screw was built and tested. The large-scale Archimedes Screw was tested for a rotations to move one liter of water, water moved per rotation, and average flow rate. The results of this testing are summarized in Table 3 and Table 4 below.
-
Figure 4: Students Using Prototypes at Zane Middle School's First Annual Galileo Day on April 3, 2015.
| Rotations to Move 1 Liter of Water | Water Moved per Rotation (Liters per rotation) | Average Flow Rate (Liters per second) |
|---|---|---|
| 152 | 0.0066 | 0.0087 |
| Setup Time (minutes) | Clean up Time (minutes) |
|---|---|
| 3.75 | 3.08 |
Components[edit | edit source]
Shown below are the various components of the Archimedes Screw Pump. Some components are depicted to show how they will fit together.
- Archimedes Screw Pump Components
-
Figure 5: Lever arm affixed to top of screw.
-
Figure 6: Pivot point located on support frame.
-
Figure 7: Tubing wrapped and fixed to screw backbone.
-
Figure 8: Pivot point mechanism.
-
Figure 9: Pivot mechanism placed inside initial reservoir.
-
Figure 10: Frame that supports screw.
-
Figure 11: Platform where terminal reservoir is located.
-
Figure 12: Terminal reservoir sitting on platform.
Discussion and next steps[edit | edit source]
The Archimedes Screw successfully transports water from an elevation of approximately 3 feet. The next step is for Joan Crandell to utilize the device in her classroom at Zane Middle School. During the final decision process the outcome of the Delphi matrix lead to a final design that was entirely different than the Archimedes Screw Pump presented above. Originally our team wanted to combine multiple water moving devices to offer many different ways of moving water. It was our participation in Zane Middle School's fist annual Galileo Day that changed this. The students at Zane's Galileo Day interacted with the prototypes and the feedback that was given strongly suggested that the students were much more inspired and interested by the screws than any of the other devices. Additionally, it was apparently obvious that the level of durability was going to require some great improvements. From this great opportunity given to us by Zane Middle School and Zane faculty, Galileo Day marked the birth of an entirely new and improved final design; a larger Archimedes Screw Pump, capable of moving larger amounts of water that will hold up for years of extensive usage to come.
Video[edit | edit source]
Team Members[edit | edit source]
Contacts[edit | edit source]
cichikawa@humboldt.edu | jcr459@humboldt.edu | ss3509@humboldt.edu | rw177@humboldt.edu
References[edit | edit source]
- Ayalon, Etan, Udi Milo, and Nes Ziona (2003). "Typology and Chronology of Water-Wheel ("sāqiya") Pottery Pots from Israel." Israel Exploration Journal 50: 216-26. Print.
- Blakemore, C. L. (1995). "Learn How Middle School Students Think." Strategies, 8, 11-14.
- Brain, Marshall. (2010). "How Aqueducts Work – A Roman Technology That Marked the Height of Their Engineering Prowess". Web. 23 Feb. 2015. <http://www.brainstuffshow.com/blog/how-aqueducts-work-a-roman-technology-that-marked-the-height-of-their-engineering-prowess/>.
- California State Board of Education. (2001) "School Safety, Discipline, and Attendence Policy #01-02 [online] Available http://web.archive.org/web/20170221220145/http://www.cde.ca.gov/BE/ms/po/documents/policy01-02-mar2001.pdf, February 25, 2015
- Cartwright, Mark. (2012) "Aqueduct." Ancient History Encyclopedia. N.p. Web. 19 < https://prezi.com/c0dxkekis1bx/ancient-roman-architecture>Feb. 2015
- Chiemi Ishiyama, Yoshito Yamamoto and Yakichi Higo. (2005). Effects of Humidity History on the Tensile Deformation Behaviour of Poly(methyl –methacrylate) (PMMA) Films. MRS Proceedings, 875, O12.7 doi:10.1557/PROC-875-O12.7.
- Crandell, J. (2015). Personal Communication. February 24. 2015, Arcata, Ca.
- Fraenkel, P.L. (1986).Water Lifting Devices. Tech. no. 43. ROME: FOOD AND AGRICULTURE ORGANIZATION OF THE UNITED NATIONS, 1986. Print.
- Fraenkel, Peter. (1997). Water-pumping Devices: A Handbook for Users and Choosers. London: Intermediate Technology, 1997. Print.
- Gratton, Luigi M., and Silvia Defrancesco. (2006). "A Simple Measurement of the Sliding Friction Coefficient." Physics Education 41.3 (2006): 232-35. IOP Science. Web. 20 Apr. 2015.
- Hodge, Trevor. (1992). "Roman Aqueducts and Water Supply."Gerald Duckworth & Co. Ltd., 1992. London. Print.
- HowStuffWorks.com. (2009), "Archimedes\\u0027 Screw" 24 August 2009 <http://science.howstuffworks.com/archimedes-screw-info.htm> 03 May 2015
- Kolle, Jefferson. (2009). "Fighting Fastener Corrosion." Deckmagazine. Professional Deck Builder, 01 May 2009. Web. 23 Feb. 2015.
- Mays, L. W. (2010). Ancient water technologies. Dordrecht, The Netherlands: Springer
- Mays, Larry W. (2015). "Irrigation Systems, Ancient." Water Encyclopedia Science and Issues. Copyright © 2007-2015 Advameg, Inc, 2015. Web. 19 Feb. 2015. <http://www.waterencyclopedia.com/Hy-La/Irrigation-Systems-Ancient.html>.
- Mujal-Rosas, R., M. Marin-Genesca, J. Orrit-Prat, A. Rahhali, and X. Colom-Fajula. (2012). "Dielectric, Mechanical, and Thermal Characterization of High-density Polyethylene Composites with Ground Tire Rubber." Journal of Thermoplastic Composite Materials 25.5 (2012): 537-59. SAGE Journals. Web. 20 Apr. 2015.
- Muller W. (1899), Die eisernen Wasserräder, Erster Teil: Die Zellenräder & Zweiter Teil:Die Schaufelräder (The iron water wheels, Part 1: the cell wheels & Part 2: the paddle wheels, in German), Veit & Comp., Leipzig.
- National Institute for Occupational Safety and Health. (2004). "Occupational Health and Safety Surveillance." Journal of Occupational and Environmental Hygiene, 1(6), D66-D67.
- Nave, Carl R. (2002) "Physical Units." Physical Units. American Association of Physics Teachers, 2000. Web. 23 Feb. 2015.
- Oleson, John P. (1984). Greek Ad Roman Mechanical Water-lifting Devices: The History of a Technology. United Kingdom and Europe: D. Reide, 1984. Print.
- Pemberton, Sonya. "Wood as an Engineering Material. (2004-2015)." - TLP Library The Structure and Mechanical Behaviour of Wood. University of Cambridge, 2004 - 2015. Web. 22 Feb. 2015.
- Russo, Ralph. (2004). "Comments (0)." Aqueduct Architecture: Moving Water to the Masses in Ancient Rome. Yale National Initiative, n.d. Web. 21 Feb. 2015. <http://teachers.yale.edu/curriculum/viewer/new_haven_06.04.04_u>.
- San Diego Plastics. Inc. (2015). "Acrylic Plastic Sheets or "Plexiglas" - Its Uses, Handling and Cutting." Acrylic Plastic or Plexiglas. San Diego Plastics. Inc, n.d. Web. 22 Feb. 2015.
- Soth, Philip, and Cindy Clendenon. (2015). "Pumps, Traditional." Water Encyclopedia Science and Issues. N.p., 2015. Web. 21 Feb. 2015. <http://www.waterencyclopedia.com/Po-Re/Pumps-Traditional.html>.
- Theodossiou, VNicos. (2014). "Evolution of Water Pumps through the Centuries with Emphasis on Hellenic Civilizations." March 2014 Web. 22 Feb. 2015. <http://www.academia.edu/8629/Evolution_of_water_pumps_through_the_centuries_with_emphasis_on_Hellenic_Civilizations
- WHO, World Health Organization. (1997). Linking Technology Choice with Operation and Maintenance for Low-cost Water Supply and Sanitation. The Hague: IRC International Water and Sanitation Centre, 1997. Print.
- Wooster, Charles B. (1942). "Plexiglas and Other Acrylic Resins." Journal of Chemical Education 19.9 (1942): 430. Journal of Chemical Education. Web. 21 Apr. 2










