The Zeer pot is a refrigeration device invented in Africa which operates by the principle of evaporative cooling. According to Science in Africa, each device can store 12kg of vegetables, keeping them fresh for up to 20 days while costing less than 2USD to produce.[1] This article will showcase how to build a pot-in-pot refrigerator, discuss various aspects of the technology and present the results of a parametric analysis.
Overview of Technology[edit | edit source]

In harsh dry climates, food preservation plays a vital role in maximizing both economic and nutritional yield from the rare opportunity of a good harvest. The dry heat significantly reduces the life of produce and as a result there is a high level of wasted crop.[2]
The following shelf-life comparison has been adapted from a case study performed by the Practical Action Organization and can be directly accessed here.
| Produce | Shelf-Life without Zeer | Shelf-Life with Zeer |
|---|---|---|
| Tomatoes | 2 days | 20 days |
| Guavas | 2 days | 20 days |
| Okra | 4 days | 17 days |
| Carrots | 4 days | 20 days |
| Arugula | 1 day | 5 days |
The impact of the pot-in-pot refrigerator is immediately realized as the shelf life for most produce is extended by 5 to 10 times. This means that farmers are not only able sell their produce beyond the initial days following a harvest, but will also be able to safely consume the unsold goods because of their extended shelf life.
Operating Principle[edit | edit source]
When evaporation occurs from a surface, there is an energy associated with the phase change known as the latent heat of vaporization. In a given system, as a gas species flows over the wet surface, evaporation and condensation continuously occur to maintain steady-state conditions.
In order to sustain evaporation, there must be a draw of internal energy in the liquid, which would result in a temperature reduction. This cooling effect is known as evaporative cooling and is most effective in dry climates due to the lack of moisture content (relative humidity) in the air.[4]
In the case of the Zeer refrigerator, water evaporates out of the sand through the surface of the outer clay pot and from the whole top surface of the moist sand exposed to the solar radiation, removing energy from the system. Figure 1 is a graphical representation of the water and energy flow within a Zeer refrigerator.
Additional information on evaporative cooling technologies can be accessed here.
How to make a Pot-in-Pot Refrigerator[edit | edit source]
The document Clay Based Technologies has been made available by the Practical Action Organization. Within the document, pages 15 to 19 outline in detail how to make a pot-in-pot refrigerator. The remainder of the document discusses other clay based technologies that may be of interest. The steps for making a pot-in-pot refrigerator are outlined below in case the reader is unable to open PDF files.[5] Alternative manuals are available based on the experience of Movement e.V. in Burkina Faso,[6] and in the Best Practices Guide based on studies in Mali done by MIT D-Lab, The World Vegetable Center and Movement e.V..[7]
- Make a small hole in the ground and cover with a mat. Use a small amount of wood chippings on the mat to prevent sticking
- Mix and knead an even mixture of mud, dung and water into a ball
- Repeatedly press a stone into the mixture to eventually form a bowl shape. Continue to do this, adding more material if necessary, until the mould reaches the dimensions given in Figure 2
- Once the mould has been made it must be left to dry in the sun for approximately 30 minutes
- Make a small hole in the ground and cover with a a mat. Use a small amount of wood chippings on the mat to prevent sticking
- Knead the clay into a dough like mixture
- Roll the clay flat and place on top of an upside down mould
- Spread the mixture over the mould, maintaining a thickness of approximately 10mm
- Use a flat stone and some water to smooth the surface
- Once the round shape has been formed the mould can be removed
- The pot walls can be extended to the desired height
- Add an extra thick layer to the rim (approximately 20mm)
- This completes the first pot
- Form the larger second pot in the same manner, using the appropriate mould
- Extend the height of this pot as needed
- Form the rim for the larger pot, using a thickness of approximately 30mm
- The final part of this process is to add decoration around the outside of the pot. This is done by rolling the mixture into a long sausage shape and sticking it around the outside of the pot about two thirds of the way up. The pattern is made by pressing fingers into it. The large pot is now complete.
- Both pots are now left in the sun to dry. This normally takes between two to four days depending on the ambient temperature and sunlight
- Identify an area that is cleared and make a circle with rocks
- Cover the ground within the circle with cow dung
- Place as many clay pots as possible inside the circle
- Completely cover the pots with wooden sticks and more cow dung
- Light the fire and let it burn for 24 hours
- To make this process more efficient it is better to burn as many pots as possible at once
- Sand should be placed in the bottom of the large pot forming a layer of approximately 5cm in depth
- Place the smaller pot on top of the sand and centre it in the large pot (the pots should now be level)
- Fill the remaining space between the pots with sand
- If possible place the assembled device on a stand to maximize air flow
- The small pot should be covered with a lid (clay or cloth) to prevent hot air from entering the storage chamber
- The pot-in-pot refrigerator operates passively as long as the sand remains moist
- Check the sand twice a day and add water as needed
Analysis of Technology[edit | edit source]
The success of the pot-in-pot refrigerator is heavily dependent on the surrounding conditions. Due to the device's reliance on natural evaporative cooling it can only be viewed as an appropriate technology for regions that demonstrate a suitably low relative humidity and a sufficient level of air flow. In order to maximize the effectiveness of the pot-in-pot refrigeration device, the rate of evaporation must be increased. To properly investigate the technology it is important to quantifying the effects of:
- Relative Humidity
- Permeability
- Flow Characteristics
- Flow Velocity
- Laminar vs Turbulent Flow
- Boundary Layer Considerations
- Area available for Evaporation
It should be noted that the values presented in the following sections indicate the maximum cooling effect for a given set of parameters. The actual cooling will likely be lower due to irregularities in parameters, such as wind speed and relative humidity.
Relative Humidity[edit | edit source]
Relative humidity is a measure of the content of water than can be held in the air at a specific temperature. An environment with a low relative humidity in comparison to one with a high relative humidity will evaporate moisture more readily and to a greater extent. For this reason, the pot-in-pot refrigeration device is only effective in environments with a low relative humidity (Figure 8). Northern central regions of Mexico (such as Chihuahua) and Africa (such as Sudan) are the most appropriate locations for use of this technology.
In some cases, the technology may prove to be suitable for specific times of the year when the humidity level is low. For a set of given conditions, information regarding humidity can be measured directly off of a psychrometric chart. Additionally, local weather centers typically keep record of humidity levels.
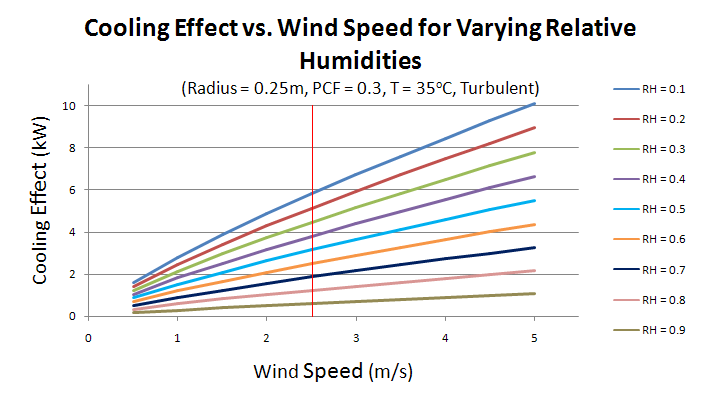
A relative humidity of 0.3 will has been used for all calculations where this value is held constant. At this relative humidity and a typical wind speed of 2.5 m/s, a cooling effect of 4.46kW is observed under turbulent flow conditions. The relationship established above, in which the device is expected to perform better in low humidity environments, is clearly indicated by this graph.
Permeability[edit | edit source]
While evaporation undoubtedly occurs through the outer clay pot, the permeability of this layer plays a significant role in determining the actual rate at which water is evaporated. Earthenware is the type of clay that is used to construct this device. This type of clay is relatively porous and permeable in relation to other forms of clay, such as porcelain and stoneware.[8] In addition to permeating through the outer clay pot, water must travel through the sand to continuously replace moisture that has passed through the clay and evaporated. The cooling effect will be limited both by this diffusion rate and the permeability of the clay.
With these considerations, a permeability correction factor of 0.3 is incorporated into the performance calculations (as detailed in Appendix A). Additionally, a graph has been produced (Figure 12) varying only this correction factor in order to provide a general insight as to how this number effects the findings presented.
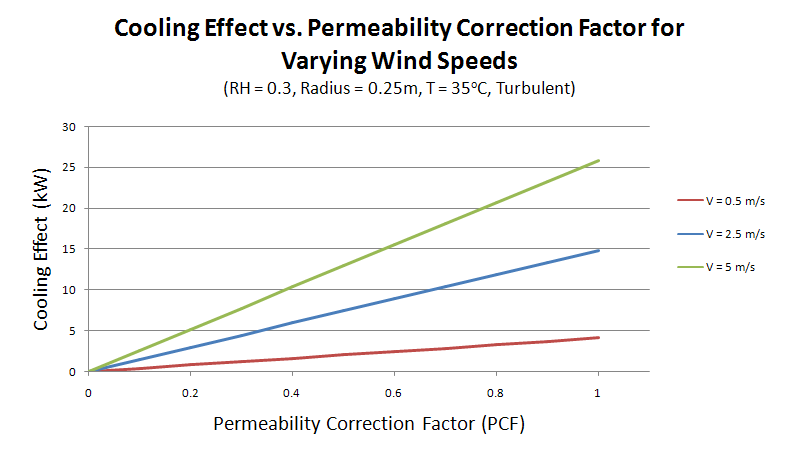
It is acknowledged that the validity of setting this correction factor to 0.3 may not be representative of the actual limitations created by the mechanisms involved with moisture diffusion and clay permeability within the device. This provides a platform for a future project to investigated this in greater detail, including the identification of methods to increase the permeability of the clay.
Flow Characteristics[edit | edit source]
Flow Velocity[edit | edit source]
As the water is evaporated into the surrounding air, the local relative humidity increases and thereby reduces the likelihood of further evaporation. Air flow is necessary to replace this moist air with dry air. This is provided by natural winds in the area. A high flow velocity will result in the body of air immediately surrounding the device to continuously remain in a dry state, and therefore will induce a higher rate of evaporation.
An average wind speed of 2.5m/s or 5.6mph has been selected based on a review of weather data for regions of Northern and Central Africa.
Laminar vs Turbulent Flow[edit | edit source]
In a given system the existence of turbulence within a fluid flow increases the level of mixing, heat transfer and mass transfer. In this particular case, for a typical setting the flow can be assumed to be turbulent. If we consider air flow over a flat plate (where the air flow is wind and the flat plate is the ground), the distance at which the flow transitions from laminar to turbulent flow can be calculated. This transition occurs for a Reynolds number of approximately 5 x .
Reynolds Number is dimensionless parameter that is defined as a measure of the ratio of inertial forces to viscous forces and can be calculated as follows:
For an ambient air temperature at 35 degrees Celsius and a wind speed of 2.5m/s, it is found that for the flow transitions into turbulence at a distance of approximately 2.6m.
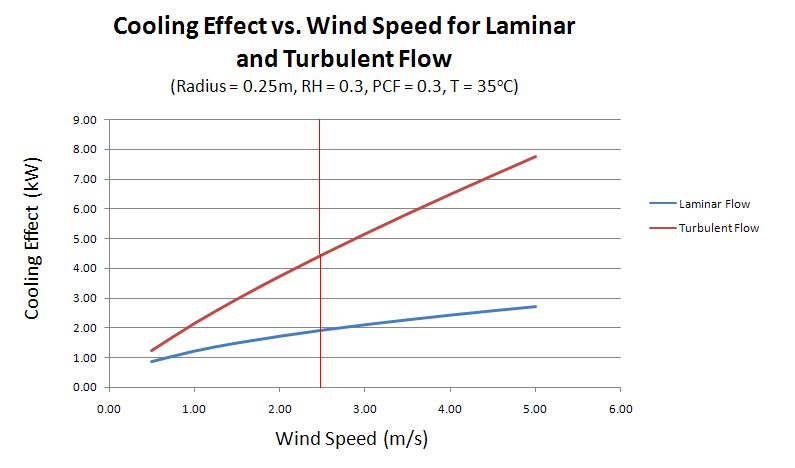
Herein lies the justification for our turbulent assumption. If we rely on natural wind, it is highly unlikely that the pot-in-pot refrigerator will be located within 2.6m of where the air flow initially interacts with the ground surface. For completeness, a graph has been produced to highlight how performance varies between laminar and turbulent flow (Figure 9).
Boundary Layer Considerations[edit | edit source]
Continuing with the flat plate analysis, the existence of a boundary layer must be acknowledged. Within this boundary layer a velocity gradient exists in which there is an increase in velocity as we move away from the ground. The actual wind velocity (free stream velocity) exists only beyond this boundary layer.[10] Due to this velocity gradient, the boundary layer height becomes an important factor that effects the performance of the pot-in-pot refrigerator. This height can be calculated as follows:
Figure 8 provides a graphical representation of how this value increases in the direction of flow. It becomes clear that by increasing the height of the pot-in-pot refrigerator, the device can be exposed to a greater wind velocity. The wind velocity has a significant impact on the performance of the device. Observation of the various graphs presented in this article indicates that their is an increase in the cooling effect as the wind speed increases.
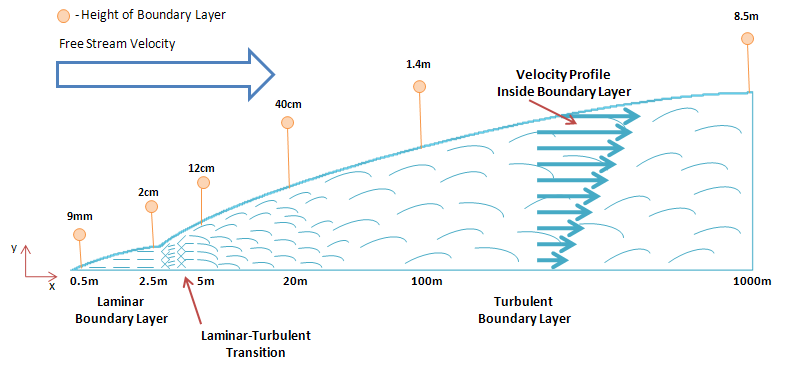
The existence of a velocity gradient within the boundary layer, and the expected performance gains due to higher velocities suggest that the device should be placed as high as possible and without obstruction of air flow. This can be accomplished by using a frame structure for the device to sit on top off. If possible, the frame itself should be placed on high ground or on top of existing solid structures.
Area available for Evaporation[edit | edit source]
The surface area available for evaporation to occur on/through can be approximated for the pot-in-pot system as:
Total Area = Surface Area of Spherical Portion of Outer Pot
+ Surface Area of Cylindrical Portion of Outer Pot
+ Surface Area of Exposed Sand in between Pots
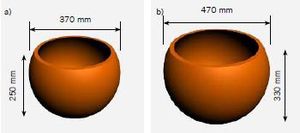
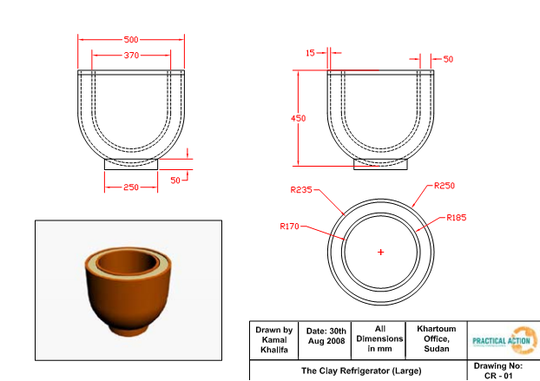
For example, if we use the recommended dimensions given by the Practical Action Organization (Figure 11), the area is found to be:
This value has been used for all calculations in which area is held constant.
Figure 12 highlights how performance of the device varies with area. An overview of the section detailing How to make a Pot-in-Pot Refrigerator, will show that the radius is the simplest dimension to vary in the process. As such, the radius of the outer pot has been selected to vary the area available for evaporation.
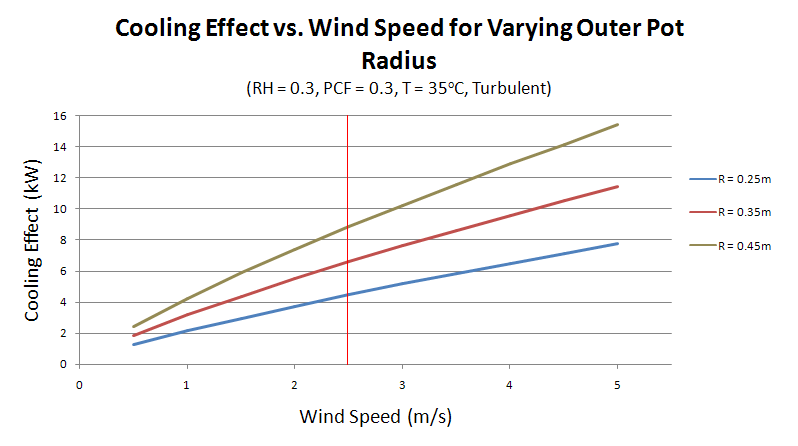
As expected, there is a noticeable increase in the cooling effect as the surface area is increased. For the chosen wind speed of 2.5m/s, there is a cooling effect of 4.46kW, 6.58kW and 8.85kW for radii of 0.25m, 0.35m and 0.45m respectively.
An increase in the area, however, implies the need to use more clay and mould material for each device, which will drive up the average price of 2USD. Additionally, the device will require more sand and more water to operate. The option to increase the area available for evaporation should only be implemented after consideration of these factors. It may prove to be a viable approach for families wishing to pool resources in order to create a larger and more effective pot-in-pot device. In this case, the inner pot should also be made larger to increase capacity of goods to be stored inside the device.
Discussion[edit | edit source]
Interpretation of Reported Values[edit | edit source]
The values for the cooling effect have been reported in kilo-Watts(kW) and not in the form of energy. The actual energy removed from the system depends on the existence of these conditions and how long they are present for.
Additionally, energy derived from this number is an indication of the total energy that can be removed from the entire pot-in-pot device. This includes both clay pots, the volume of sand, water content within the sand, the air within the storage chamber and the contents of the storage chamber. The value therefore, should not be interpreted as the energy withdrawn exclusively from the storage chamber. A complex conduction and mass diffusion model would be required to provide a full analysis of the heat transfer mechanisms within the pot-in-pot structure, which falls outside the scope of this article.
Convection[edit | edit source]
The pot-in-pot refrigerator will experience both forms of convection. When the air is idle the device will experience natural convection and subsequently, when the air is moving at a given velocity, the device will undergo the effects of forced convection.
In both cases it is likely that the convective process will transfer energy to the system due to the high ambient temperature and cooler device surface temperature. This energy that is transferred into the system will reduce the overall cooling effect. In comparison to the energy associated with a change of phase reaction (evaporation) however, the convective losses/gains are relatively small.
Radiation[edit | edit source]
The Zeer pot refrigerator is expected to operate in open conditions with exposure to direct sunlight during the day. This will transfer a significant amount of energy to the system, reliant on the level solar irradiation, surface temperature of the outer pot and material properties of the clay.
Rough Approximation for Net Energy Balance[edit | edit source]
This section will attempt to quantify the amount of energy withdrawn from the storage chamber by applying an energy balance including evaporative cooling and radiation.
The following conditions describe the base case scenario used throughout the article:
To include the effects of radiation let us consider only daylight hours, assumed to be between the 8am and 6pm (10 hours).
The maximum cooling effect for the parameters listed above was reported to be 4.46kW. Over the course of 10 hours, the overall cooling (considering periods of flow stagnation, environmental irregularities, and periods of reduced of moisture content in the sand) has been approximated to be equal to three hours at this maximum value for the prescribed conditions. This gives us an effective energy loss from the system of 13.4kWh.
The following calculation determines the net energy transfered to the system by radiation for the described scenario. Additionally let:
Performing an energy balance on the device (only for radiation):
=
We can approximate the area exposed for radiative on heat transfer equal to:
Over an exposure period of 10 hours the total net radiative energy transferred to the system is 1.92kWh.
Therefore, the energy flowing out of the device over a period of 10 hours is found to be (13.4 - 1.92) = 11.48kWh
As mentioned above, this value represents the energy loss for the entire pot-in-pot device. Due to the nature of conduction, a temperature gradient within the device must be present to create an out-flux of energy. Each layer of the device therefore must be cooled: the outer pot; volume of sand; water content within the sand; inner pot; air within the storage chamber; and the contents of the storage chamber. Taking this into consideration, it is reasonable to estimate that the only 5% of the total energy out-flux directly impacts the storage chamber.
Therefore, the actual cooling within the storage chamber for the prescribed conditions is found to be roughly 0.57kWh.
Limitations of Device[edit | edit source]
Beyond the limitations of the required climatic conditions for the pot-in-pot refrigerator to be successful, there is also a need for a continuous supply of water. For many regions, water may be prioritized for other purposes making the it difficult for communities to adopt the technology. The device also has no proper seal for the storage chamber, reducing it's overall effectiveness since warm ambient air can seep into this chamber and increase the temperature of chilled zone. (however warm air will rise and chilled air is heavier and drops, so the temperature will always be coldest on the bottom)
Conclusion[edit | edit source]
A parametric analysis concerning the performance of a Zeer pot-in-pot refrigeration device has been performed. As expected, the device performs well only in climates possessing a low relative humidity. The velocity of the wind and the area available for evaporation to occur on/through are two primary factors that can be addressed to improve the performance of the pot-in-pot refrigerator.
It has been shown that increasing the radius of the outer pot from 0.25m to 0.45m, almost doubles the total cooling effect. The adaptation of this however, is restricted by the increase in cost associated with using more materials. It is suggested that the strategy to make larger pot-in-pot refrigerators be employed only if community members are willing and able to pool their resources to share a device with superior performance.
It is unrealistic to assume that electricity is available to ensure that their is a constant and adequate source of air flow. The device is dependent solely on naturally occurring winds. To maximize air flow, it is recommended that Zeer refrigerator be placed as high above the ground as possible. This can be accomplished by building a simple frame to support the device, and placing them on high ground or on top of buildings.
There remains the potential for future analysis of this device. The development of a detailed conduction model to analyse heat transfer and mass diffusion mechanisms within the various layers would aid in identifying factors limiting performance and how they can be addressed. Additionally, by experimentation, a study could be performed to replace the permeability correction factor used in this analysis with real diffusion rates of moisture through clay.
References[edit | edit source]
- ↑ Elkheir, M., "The Zeer Pot - a Nigerian invention keeps food fresh without electricity", Science in Africa, 2002
- ↑ Elkheir, M., "The Zeer Pot - a Nigerian invention keeps food fresh without electricity", Science in Africa, 2002
- ↑ Practical Action Organization, "How a zeer pot fridge makes food last longer", 2009, http://web.archive.org/web/20150827110344/http://practicalaction.org:80/home/zeerpots
- ↑ Committee on Microgravity Research; Commission on Physical Sciences, Mathematics and Applications; "Microgravity Research in Support of Technologies for the Human Exploration and Development of Space and Planetary Bodies", Space Studies Board, National Research Council, 2000
- ↑ Practical Action Organization, "Clay Based Technologies", 2007
- ↑ http://www.movement-verein.org/downloads/Movement_Clay-pot-cooler_english.pdf
- ↑ https://d-lab.mit.edu/sites/default/files/inline-files/Evaporative%20Cooling%20Best%20Practices%20Guide.pdf
- ↑ The Clay Room, Telephone Interview with Representative, 2010
- ↑ Incropera, F.P., Dewitt, D.P., Bergman, T.L., Lavine, A.S., "Fundamentals of Heat and Mass Transfer", John Wiley and Sons, 2007
- ↑ Incropera, F.P., Dewitt, D.P., Bergman, T.L., Lavine, A.S., "Fundamentals of Heat and Mass Transfer", John Wiley and Sons, 2007
- ↑ Incropera, F.P., Dewitt, D.P., Bergman, T.L., Lavine, A.S., "Fundamentals of Heat and Mass Transfer", John Wiley and Sons, 2007
- ↑ Incropera, F.P., Dewitt, D.P., Bergman, T.L., Lavine, A.S., "Fundamentals of Heat and Mass Transfer", John Wiley and Sons, 2007
Appendix A: Calculation Methodology[edit | edit source]
All equations have been solved used the software package EES (Engineering Equation Solver). The equations used are outlined below.
- Given,
- Outer_Clay_Pot_Radius = 0.25 m
- Inner_Clay_Pot_Radius = 0.185 m
- Thickness = 0.015 m
- Height = 0.45 m
- Ambient Temperature = 308 K
- Ambient Pressure = 101.3 kPa
- Wind Speed = 2.5 m/s
- Relative Humidity = 0.3
- Permeability Correction Factor = 0.3
- Fluid Properties,
- Density of Air acquired as a function of T and P
- Viscosity of Air acquired as function of T
- Density of Water acquired as a function of T and P
- Density of Water Vapour acquired as a function of T, P and RH
- Latent Heat of Vaporization for Water = 2270 kJ/kg
- Diffusion Coefficient of Water into Air (D) =
- (Curve Fit by Boltz and Tuve 1976)
- Manipulations,
- Area:
- Reynolds_Number:
- where,
- (Lchar for exposed sand + Lchar for outer clay pot)
- (Length of exposed sand along diameter of device + Maximum circumference of device)
- where,
- Schimdt_Number:
- Avg_Sherwood_Number(Laminar):
- Avg_Sherwood_Number(Turbulent):
- Coeff_MassTransfer: (Employing Heat and Mass Transfer Analogy)
- Evap_Rate:
- Evap_Cooling: