Background[edit | edit source]
Catherine Zane Middle School in Eureka, California, has partnered with the Engineering Design course at Cal Poly Humboldt in order to provide an opportunity for students to exercise their skills in sustainable engineering design. Our project team is called Division by Zero. Team members include Hannah Gidanian, Caitlin Gundert, Rick Thomas, and Alex Watson. The front of Zane Middle School features a large rectangle filled with bark mulch, 10 feet wide and over 100 feet long. This empty space receives a large amount of uninterrupted sun throughout the day. Zane wanted to improve this underutilized space and decided that a series of projects would be conducted by the Engineering Design class of Spring 2017.
Problem Statement and Criteria[edit | edit source]
Students at Zane Middle School currently do not have an interactive and tangible way to learn about the abstract idea of how the sun relates to the earth and the concept of time as a derivation of this relationship. There is a large, vacant section of the front of the school at Zane that has not been serving any purpose over the past several years. As a result, the bark mulch gets trampled across, leaving debris all over the pavement in front of the school.
| Criteria | Importance | Constraints |
|---|---|---|
| Durability | 10 | Withstands abuse from students and elements while lasting at least 20 years |
| Safety | 9 | Must follow all safety regulations designated by the school. |
| Educational Value | 8 | Must be able to be used as a teaching tool for the teachers |
| Multiple Time Components | 7.5 | Can tell the month along with the time |
| Cost | 6.5 | Total budget of $400 |
| Accuracy | 6 | Correct time and months |
| Interactivity | 6 | Gets the child engaged and interacting with the sundial |
| Aesthetics | 5 | Visually pleasing |
| Sustainability | 4 | Constructed of environmentally friendly materials |
| Precision | 3 | Recognizable time values |
The Solution: Description of Final Project[edit | edit source]
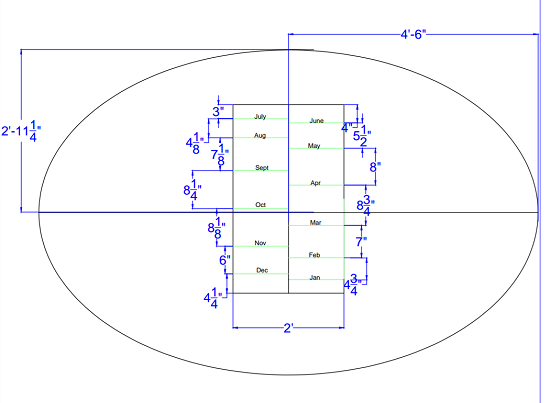
A group of four Engineering Design students, by the team name of "Division by Zero" have partnered up with Trevor Hammonds and Kristopher Buihner at Zane Middle School in order to implement an interactive and aesthetically pleasing addition to the school front, directly in the center of the previously barren rectangle filled with bark mulch. The analemmatic sundial is stamped in a 9'x10' platform of cement on which middle school children serve as the gnomon. The student's shadow will tell the solar time. This sundial will serve to provide middle school students with an educational activity to emphasize the concept of solar time and the interaction between the sun and the earth in its orbital path.
Costs[edit | edit source]
| Materials | Quantity | Cost Per Quantity $ | Our Cost $ |
|---|---|---|---|
| Table Cloth | 1 | 17.99 | 17.99 |
| Canvas | 1 | 29.99 | 29.99 |
| Dowels | 2 | 0.69 | 1.38 |
| Wood Letters | 6 | 3.99 | 23.94 |
| 1x2 Furr Trim | 1 | 30.99 | 30.99 |
| 1/4 in Plywood | 1 | Donated | Donated |
| Wood Glue | 1 | 4.99 | 4.99 |
| Sand Paper | 4 | 0.79 | 3.16 |
| Total Cost | $112.44 | ||
8th grader Keylei and School Psychologist Trevor Hammons with the final sundial
Amount of hours the team members spent. Total Hours:227
Prototyping[edit | edit source]
Many prototypes were made before placing the sundial in concrete. Prototyping on a canvas sheet proved effective.
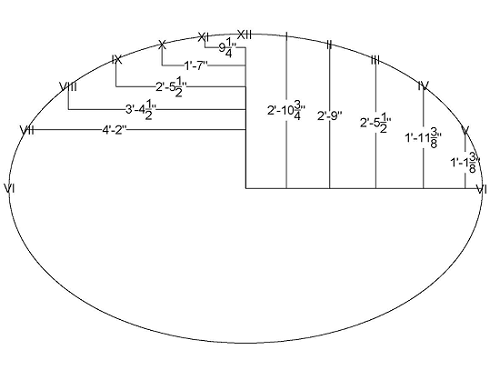
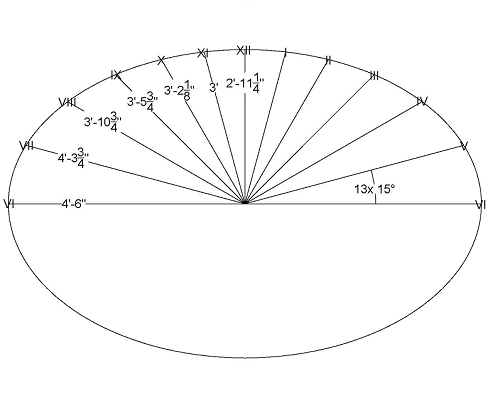
Calculations[edit | edit source]
| Step | Description | Picture |
|---|---|---|
| 1 | First, find the dimensions of the space where the sundial will be placed. Then find the latitude and longitude of the location. After this is done, the ellipse of the sundial needs to be created. Use the length of the space available to find the major axis of the ellipse. The minor axis can be based on the average height of humans that will be using the sundial. To find the length of the minor axis, the length of a person's shadow at 12:00 needs to be calculated. The equation to do this is
m=Msin(phi) Where: m= Minor axis M= Major Axis phi= latitude of location in degrees After the minor and major axis are found, plug them into the ellipse equation: (x^2/M^2)+(y^2/m^2)=1 Where the x and y are the xy coordinates. Calculations were done with a latitude of 40.7892 Major Axis:9 ft Minor Axis:2 ft 11.25 in |
.png) |
| 2 | Each number on the sundial is 15 degrees from the positive x-axis, and the XY values of the numbers for the time were found using the ellipse equation.
Radial units were then found by using sin(theta)=opposite/hypotenuse. |
.png) |
| 3 | The place where a person stands (the scale of dates) is based on the Analemma, which is the path of the sun in the sky over the year. To find the distance for where to stand for each month using the equation:
Z=Mtan(d)*Cos(theta). Z is the distance from the origin M is the horizontal radius of the ellipse d is the declination for each month theta is the latitude in degrees |
 |
| 3 | Each of the season lines which are plotted into the cement is based upon the shadow length at each hour of the day throughout the year. The shadow length was calculated by taking the tangent of the angle of elevation of the sun at each hour of the day on the equinoxes as well as the solstices. Using right triangle trigonometry, it was determined that the shadow length equates to the height of the pole (24") divided by the tangent of the mentioned angle. |  |
Construction[edit | edit source]
How to Use it[edit | edit source]
To find the current solar time, stand in the box with the current and corresponding month. Depending on what date it is within the month, you may need to alter where you stand within the box. If it is early in the month, stand on the bottom line of the box; if it's the middle of the month, stand in the middle of the box, and if it's the end of the month, stand on the top line of the box.
Measure the shadow length on two consecutive days at the same time. If the shadow length appears to be shrinking and falls between the equinox line and summer solstice line, the present season is Spring. If the length appears to be growing and is in the same location, it is Summer. If the shadow location is between the winter solstice and equinox line and appears to be growing, the present season is Fall, and if the shadow is shrinking, the season is Winter.
Maintenance[edit | edit source]
- Monthly
- Rinse the imprint of the numbers with water to keep the sundial clean and the numbers visible.
- Yearly
- Sundial season lines may need to be repainted depending on the rate of degradation.
