Math path project at Catherine Zane Middle School where the main theme is the Fibonacci spiral containing geometry contents. The project was designed by the Avengineers team of the Engineering Design 215 intro to design course at Cal Poly Humboldt, taught by Lonny Grafman in Spring 2021. The target audience of the math path were the math and science students of Zane Middle School struggling with certain topics such as calculating geometric areas. The Team was excited to find an artistic approach to commonly difficult mathematical concepts and find a way to make learning about math more enjoyable.
Background[edit | edit source]
Our team is made up of CPH Engineering 215 students Steven Camara, Minh Truong, Avery Tunnicliff in the Spring Semester of 2021. Our client for this project is Catherine. L Zane Middle School, a STEAM based middle school located in Eureka, CA. Our team, the “HSU Avengineers”, worked directly with the 7th grade math program’s Instructor, Terra Pennsy. The main entrance of the school needed beautification and is the home of our project.
Problem statement[edit | edit source]
The objective of this project is to design and build an educational math aesthetic on the landscape of Zane Middle School’s campus that will inspire students in 6th-8th grade math classes. Furthermore, our team wanted to provide a way for students to see and understand relevant math concepts in ways other than textbook problems.
Below is a list of our weighted criteria which was based on and created with our client. The criteria are listed by levels of importance and have corresponding constraints for each.
Criteria:
| Criteria | Description | Weight (1-10) |
|---|---|---|
| Safety | Project must be safe and meet required standards of health and safety of Zane Middle School. | 10 |
| Educational Value | Project must have educational value for students that interact with it. | 9 |
| Aesthetics | Project should be visually suitable to the themes and aesthetics of Zane Middle School. | 8 |
| Level of Inspiration | The function of the project should promote the interest of students in learning and applying mathematical concepts | 8 |
| Accessibility | Project should be physically and mentally accessible and inclusive to all ranges of students that could use the path. | 7 |
| Durability | Project should be able to withstand environmental conditions (including usage by students and the weather at Zane Middle School). | 7 |
| Interactability | Students should be able to interact with the project in some way that goes beyond visual observation. | 6 |
| Cost | The cost of the project should not exceed $300 | 6 |
Prototyping[edit | edit source]
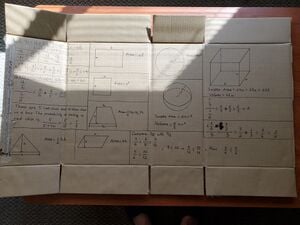
Some of our early prototyping designs are Computation Conflict, Math Land, Fibonacci spiral, Cheat Sheet, etc.
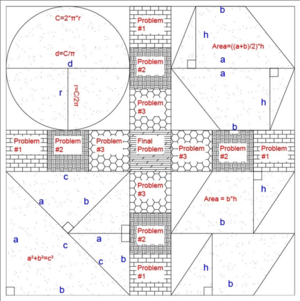
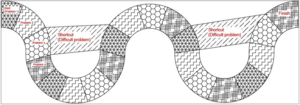
We, then, had three prototypes that were examined outdoor in practicing. They were the Fibonacci Geometry, the Cheat Sheet, the Computation Conflict.
We tried two methods of making the design appeared on concrete. One is imprinting and the other one is painting.
After considering relative conditions, our team decided to choose the painting method.
Final product[edit | edit source]
After showing our clients the alternative prototypes, we decided to conglomerate the separate solutions into one final design, naming it "The Fibogeometry".The team also decided to paint the final design, and create it in a way that is easily replicable through a series of stencils. The final design has three main rectangles which contain Fibonacci spirals. The middle rectangle is filled with various geometric shapes, and the corresponding equations to solve each. The two opposite rectangles have been left relatively blank, to allow students to experiment with shapes creatively through means of drawing with chalk on the concrete.
Construction[edit | edit source]
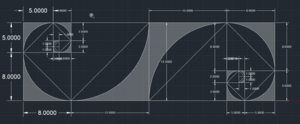
- Referencing the CAD design, used a tape measure and a chalk line to draw out all the 2” lines that make up the 3 rectangles
- Used duct tape and the chalk guides to mark out 2” lines of Fibonacci squares
- Used white paint to completely paint inside of taped areas
- Allowed paint to dry for 6 hours and then applied 2nd coat
- Peeled off duct tape
- Used aluminum stencil to mark out Fibonacci spirals
- Painted with red paint and a hand brush. Reapplied after 6 hours.
- Used paper letter stencils and red paint formulas on center spiral. Reapplied after 6 hours.
- Sample gallery
-
Removing Tape
-
-
-
-
-
-
Minh Truong- Holding the opposite end of a chalk line being used to mark out where the duct tape and paint needs to go.
Video instructions[edit | edit source]
Bill of materials[edit | edit source]
Below is the table for the the materials used in this project and their cost.
| Item | Amount | Cost per unit | Total |
|---|---|---|---|
| Concrete Stepping Stones 12" x 2" x 12" — Ace Hardware | 4 | USD 2.49 | USD 9.96 |
| Prototyping Paint — PPG Paints | 2 | USD 5.75 | USD 11.50 |
| Paint Roller — PPG Paints | 2 | USD 4.55 | USD 9.10 |
| White Plastic Paint Pan — PPG Paints | 2 | USD 3.25 | USD 6.50 |
| Paint Brush — PPG Paints | 2 | USD 2.39 | USD 4.78 |
| Paint Roller Cover — PPG Paints | 2 | USD 2.31 | USD 4.62 |
| Aluminum Stencil 4'x5' (0.063" thick) — O&M Industries | 1 | USD 130.15 | USD 130.15 |
| Concrete Stain Paint — PPG Paints | 2 | USD 40.75 | USD 81.50 |
| Duct Tape — PPG Paints | 3 | USD 5.99 | USD 17.97 |
| Chalk Line — Ace Hardware | 1 | USD 8.75 | USD 8.75 |
| Grand total | USD 284.83EUR 244.95 <br />GBP 207.93 <br />CAD 353.19 <br />MXN 5,938.71 <br />INR 21,319.53 <br /> | ||
Operation[edit | edit source]
This section will briefly cover how to use the Fibogeometry Math Path and the contents within.
Path use:
The path is designed to be aesthetically pleasing regardless of the contents within, and can therefore be walked and enjoyed easily. In terms of mathematical concepts, shapes within the spirals can be calculated using Fibonacci's golden rule; as the lengths of the squares increase proportionally in respect to the spirals, so can the areas and parameters of any other shapes within.
Maintenance[edit | edit source]
The section below covers the frequency and steps as pertaining to the maintenance of the Fibogeometry Math Path.
Schedule[edit | edit source]
The Fibogeometry Math Path will need maintenance about every 3-5 years.
Instructions for Maintenance[edit | edit source]
Use duct tape/outdoor tape to line the outsides of the existing paint to prepare for a re-coat of the straight white lines. The margin between the tape should be 2 inches.
Using a small roller or spray machine evenly apply the white concrete paint to the areas that have been prepped with tape.
Wait 1 hour for the paint to dry before removing the tape.
Starting from the ends of the spiral in the corners of the larger squares of each section, line up number 1 on the stencil with the corner and then use the brush and red paint to paint within the stencil. Then move to the middle rectangle, and then the last rectangle, repeating that step, wiping excess red paint off of the stencil with a rag.
Repeat the cycle of using the next number on the aluminum stencil and visiting each section of the path starting from one side, going to the middle rectangle, and then the last with each consecutive number on the stencil. (RectLeft, RectMiddle, RectRight, RectL, RectM, RectR…etc.).**(Note: Stencil 1 will need to be used 4 times end to end, and stencil 2 two times end to end on each)**
Conclusion[edit | edit source]
Testing results[edit | edit source]
Due to a later implementation period, the final design has yet to be tested by students. However, the tests that our team were successful and met our goals.
Discussion[edit | edit source]
After extensive testing from the team, we determined that our final design and implementation were a success, and made learning enjoyable overall.
Lessons learned[edit | edit source]
One of the most important lessons we learned as a team, was how aggressive communication needs to be towards the design and implementation portion of a project. The clients want our help, and sometimes it just takes a little extra nudge to get the information and guidance a project can depend on.
Next steps[edit | edit source]
Future steps for this project lie in the instructions and stencils created by the team. By using the stencil from our final design, the path can be replicated virtually anywhere.
Troubleshooting[edit | edit source]
The table below depicts the general steps for basic trouble Shooting with the Math Path.
| Problem | Suggestion |
|---|---|
| Lining up the spiral stencil | Refer to figure above containing curve/stencil number and its corresponding placement in the path. |
| Finding the direction of the curve in each reactangle | Refer to the 'Fibogeometry' figure above listed within the Final Design portion of the document |
Team[edit | edit source]
Below is a list of the members of team Avengineers for Lonny Grafman's Spring Engineering 215 class at HSU (2021):
- Avery Tunnicliff
- Steven Camara
- Minh Truong
