In some scenario of human underwater activity, it is too dangerous for crew members to manipulate the underwater vehicle. At this circumstance, underwater unmanned vehicle (UUV) is needed. To maintain the stable movement of the UUV, a robust control system is specifically needed. One of the most mature control system for UUV uses PID control as feedback control. PID control is an autonomous control method, it provide robust control against disturbance. However, PID control is not optimal for UUV, since it's a passive control method. Thus, fuzzy logic control system will be introduced in the feedback system for UUV to create a fuzzy interference system (FIS). Fuzzy logic control system is an expert system. Based on preset rules, it can provide well planned solution according to real time input as parameters. However PID still have mature solution against disturbance and dealing with oscillation problem, considering this, PID control method will be used as one subset for the FIS sets, especially when desired stats is quite close to current states.
In this project, we will use Mamdani type of FIS,[1] creating state space model for UUV and define fuzzy controller. And pure PID control system will be compared to this FIS as a result.
Project goals[edit | edit source]
- The goal of the project is to design a fuzzy logic controller which would be used to control a underwater unmanned vehicle (UUV).
- This fuzzy logic controller would work in sidelines with a PID controller to control the underwater unmanned vehicle.
- The main aim of the fuzzy logic controller is to control the depth, direction and speed of the underwater unmanned vehicle. The depth would be controlled by the central fins of the UUV, the direction would be controlled by the rear tail fins of the controller. Now a UUV in general is controlled by using PID controllers but because of it being less optimal and not able to respond more efficiently. Thus using a fuzzy controller would provide with the required results and output of the UUV in a more efficient and rapid manner. This is because the fuzzy logic controller can be used to design complex control system and with effectively fast results as the fuzzy logic controller follows the concept of a rule based system, in which we convert the real world system of inputs to data inputs. In this the inputs would go through a set of rules.
- For a UUV the set of inputs would be the desired direction, desired speed and desired depth. Thus these inputs would be compared to the fuzzy sets values and corresponding to those desired outputs would be given considering the working mathematical model of an actual UUV.
- Now a PID controller of a UUV would be based on a Non Linear system as there are three systems that are associated with the submarine, the altitude, direction and third being the speed, thus the PID controller basically learns its way to the desired output thus not being effectively fast. But a PID controller is required with a Fuzzy logic controller because the Fuzzy logic controller even after giving the desired output might not be able to stop the output on time, say for example if we need to control the depth of the UUV and lower the depth by 70 feet and on using the fuzzy logic controller the submarine may surpass the limit of 70 feet and might go below 70 feet by few feet and would then again increase the altitude in water and thus the UUV's altitude might oscillate about the 70 feet depth. Thus would surely be a bumpy ride for the UUV and would cost a lot of fuel. Thus a PID controller could be used in such a situation.
- The fuzzy controller can be used in sidelines with a PID controller by at first using the fuzzy controller to give the required direction and magnitude to the output and which would effectively improve the effective response of the UUV to the inputs and when the submarine almost reaches to its required final state by a certain already prescribed limit (which will be small) then we could switch over the control system to a PID controllers so that the UUV could have a smooth transition to the required direction, altitude or speed without any oscillations about the required result.
- Be able to control the altitude, speed and direction of the UUV if changed suddenly due to underwater currents or turbulence thus bringing the drifted submarine back to its path
Method[edit | edit source]
General approach[edit | edit source]
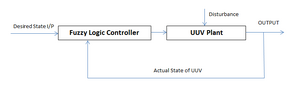
- A closed loop system is developed in which the fuzzy logic controller is supplied with both the desired and actual states of the submarine. Here, we compare the actual state of the submarine with the desired state of the submarine and then generate a command to the Underwater Unmanned Vehicle Plant (UUV Plant) by using fuzzy logic Controller. The command generated should drive the Plant into its desired state. The fuzzy logic controller should be designed in such a way that it should minimize the error in the parameters of UUV plant.
- An error to the parameters of a UUV Plant can be caused due to the disturbances in the surrounding environment which can change both in direction and magnitude continuously. External disturbances can be Sea currents, heat over the sea surface, etc. For example, consider that an underlying sea current is trying to change the direction of our plant continuously in a random way. Now the fuzzy logic controller to be developed must counteract the changes in the direction of UUV plant immediately, So that the plant moves in the desired way.
- Basic Parameters that we need to control could be the speed, direction and altitude of the vehicle. By knowing the desired speed and actual speed of the vehicle, the controller should be able to increase or decrease the actual speed of the vehicle. A fuzzy logic controller could be more effective here considering the rapid and random changes that can be caused by the surrounding environment.
- The main requirement of this control system is that the submarine should attain desired direction not only in ideal conditions (no external environmental disturbances) but also perform well in presence of external environmental disturbances and adapt its parameters intelligently according to varying operating conditions. Here, we are implementing the simulation of this model using MATLAB. The UUV plant is virtually created by using the state space model of a submarine.
- Now, the UUV plant is disturbed by a signal which would correspond to a sea current and then the functioning of the plant is observed. If the plant is not influenced by that external disturbance, then it would correspond to the effective functioning of the fuzzy logic controller.
Underwater unmanned vehicle model[edit | edit source]

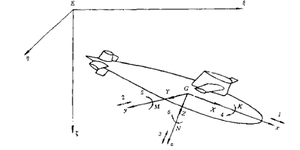
In order to investigate the controllability of the UUV, descript the position and posture. We will use two right-hand coordinate system. E-ξηζ,which is a coordinate system fixed on the planet and G- xyz is a coordinate system move with the UUV.
The origin of the fixed coordinate system E, can be placed to any point on the planet, the plane E-ξη is parallel to the horizontal plane, the axis E-ζ is perpendicular to the plane E-ξη and point to the earth's core.
The origin of the coordinate system, G, is placed on the center of gravity of the UUV. The axis Gx, Gy, Gz are intersection lines between horizontal plane, sheer plane and transverse cross-section plan, respectively.
The velocity of the center of gravity relative to the fixed coordinate is V, the projection of V on G-xyz are (u,v,w). Similarly, the angular velocityΩproject to G-xyz are (p,q,r). The total external force applied to the UUV is F, and its projection on G-xyz are (X,Y,Z). The total moment applied to the UUV is M, and its projection on G-xyz are (K,M,N).
Anticipated Results[edit | edit source]
- The Control system of the UUV be sensitive and fast in response.
- Give an accurate and quick response at the beginning and be able to stabilize itself at the required output in the end.
- UUV be able to stabilize itself quickly at uncertain conditions underwater like currents or turbulence which would drift the submarine from its present condition.
Literature review[edit | edit source]
Fuzzy Logic Controller for Submarine[edit | edit source]
Reviewed by Du Zhaoxu
This paper introduces general fuzzy logic control method for a submarine moving in plane parallel to the earth surface. Paper give both simulation in ideal situation with no disturbance and in presence of sea currents.
Paper give brief introduction of concept of fuzzy logic control method, describe it as 'expert' system, and brings fuzzy interference system (FIS) into the control system of submarine. As one of FIS system, Mamdani type of FIS system is used in this paper.
Paper first set up submarine models using linearized state space model. This model is further modified, considering sea currents as disturbance, according to linear superposition theorem.
Then, accordingly, desired state model is built to give the difference as input. As core content, paper define three stage for fuzzy controller system: input stage, processing stage and output stage. For input stage, according to the submarine model, heading error and heading rate are used as input data. For output stage, rudder deflection is considered as output data. All these three data are fuzzificated into variables of membership functions according to the table of 'Member functions of variables'. Then rules are define for each vector of fuzzificated inputs. Totally, the number of rules should be: (number of membership function)^(number of inputs). After rules are set, output can be searched accordingly. At last output should be defuzzificated into executable data.
Simulation for this model shows stable control result.
Paper does not consider vertical motion model. However, vertical motion model can be separately built and composited with horizontal plane movement.
A Novel Fuzzy Logic PID Algorithm for Submarine Hydraulic Rudder Control[edit | edit source]
Reviewed by Du Zhaoxu
Downloadable content[edit | edit source]
Paper[edit | edit source]
- For current draft, click here
FISes[edit | edit source]
Simulink model[edit | edit source]
- For simulink model, click here
Data[edit | edit source]
- For the code to generate training data of rudder as output for FIS1, click here
- For the code to generate training data of stern as output for FIS2, click here
Bibliography[edit | edit source]
- Orhan K Babaoglu, George J Thaler "Designing of an Automation control system for a Submarine", Naval Postgraduate School, AD-A203 925
- Ridley, Peter, Fontan, Julien, & Corke, Peter (2003) Submarine automatic control. In Roberts, Jonathan & Wyeth, Gordon(Eds.) Proceedings of the 2003 Australasian Conference on Robotics & Automation, Australian Robotics & Automation Association, Brisbane
- Ridley, Peter, Fontan, Julien, & Corke, Peter (2003) Submarine dynamic modelling. In Roberts, Jonathan & Wyeth, Gordon(Eds.) Proceedings of the 2003 Australasian Conference on Robotics & Automation, Australian Robotics & Automation Association, Brisbane