Jatropha curcas belongs to the family Euphorbiaceae and is thus closely related to other important cultivated plants like rubber, castor etc. It is believed to be a native of South America and Africa but later spread to other continents of the world by the Portuguese settlers. The Arabs have been using this plant for medicinal purpose. Today it is found in almost all the tropical and sub tropical regions of the world.
There are more than 200 names for it all over the world, which indicates its significance to man, and the various possibilities of its use. In India, Jatropha curcas is found in almost all the states and is generally grown as a live fence for protection of agricultural fields from damage by livestock as it is not eaten by cattle or goat.
Botanical features[edit | edit source]
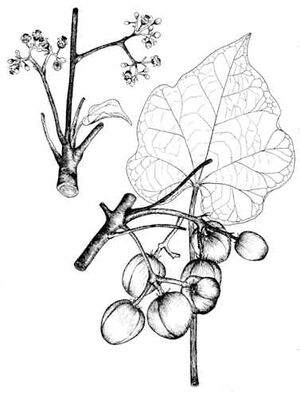
It is a small tree or shrub with smooth gray bark, which exudes a whitish colored, water, latex when cut. Normally, it grows between three and five meters in height, but can attain a height of up to eight or ten meters under favourable conditions.
Leaves[edit | edit source]
It has large green to pale-green leaves, alternate to sub-opposite, three-to-five lobed with spiral phyllotaxis.
Flowers[edit | edit source]
The petiole length ranges between 6-23 mm. The inflorescence is formed in the leaf axil. Flowers are formed terminally, individually, with female flower usually slightly larger and occur in the hot seasons. In conditions where continuous growth occurs, an unbalance of pistillate or staminate flower production results in a higher number of female flowers.
Fruits[edit | edit source]
Fruits are produced in winter when the shrub is leafless, or it may produce several crops during the year if soil moisture is good and temperatures are sufficiently high. Each inflorescence yields a bunch of approximately 10 or more ovoid fruits.
A three, bi-valved cocci is formed after the seeds mature.
Seeds[edit | edit source]
The seeds become mature when the capsule changes from green to yellow, after two to four months from fertilization. The blackish, thin shelled seeds are oblong and resemble small castor seeds.
Ecological Requirements[edit | edit source]
Jatropha curcas grows almost anywhere- even on gravely, sandy and saline soils. It can thrive on the poorest stony soil. It can grow even in the crevices of rocks.
The leaves shed during the winter months form mulch around the base of the plant. The organic matter from shed leaves enhances earthworm activity in the soil around the root-zone of the plants, which improves the fertility of the soil.
Regarding climate, Jatropha curcas is found in the tropics and subtropics and likes heat, although it does well even in lower temperatures and can withstand a light frost. Its water requirement is extremely low and it can stand long periods of drought by shedding most of its leaves to reduce transpiration loss. Jatropha is also suitable for preventing soil erosion and shifting of sand dunes.
Cultivation practices[edit | edit source]
It can be easily propagated on massive scale by direct seeding as well as planting stem cuttings. Hot and humid weather is preferred for good germination of seed. Plants bear fruits in the beginning of winter. Approximately 5-6 kgs. of seed is adequate to raise one hectare of plantation. The spacing maintained is about 2m x 2m and for high density planting 2m x 1m distance can be recommended.
Seeds or cuttings can be directly planted in the main field. Some times the seedlings are grown in poly bags and then transplanted in the main field. The land should be ploughed once or twice depending upon the nature of soil. In direct planting system the seed/cuttings should be planted in the main field with onset of monsoon at a spacing indicated above. Apart from organic manure, mixtures, fertilizers containing NPK should be applied near the planting hole. To keep the land free from weeds in the initial stage, 3-4 hand weedings are necessary; it does not require supplementary irrigation. However, the approximate yield of 1200 kg seed per hectare may be obtained from irrigated plantations in comparison to 750 kg seed (per hectare) from rainfed plantations. This is expected from 3rd year onwards. The economic life of the plant is about 35-40 years. Jatropha oil is extracted by hydraulic press method after grinding and steaming of the seed.
Commercial uses of the Plant[edit | edit source]
The increasing gap between demand and supply of fuel wood leads to fast depletion of forest cover. There is need to search for alternative source of energy derived from non-wood sources. For this purpose high density plantation of Jatropha, as an energy crop, may provide energy on regular basis annually for a period of 40-45 years without replanting, unlike other fuel wood crops. With suitable technology, jatropha could possibly be used as furnace fuel to facilitate electricity generation in a decentralized manner and at a lower cost as compared to the existing power generation system, which requires massive infrastructure for distribution of power.
Besides the above, the following additional benefits can also be expected:
- Jatropha oil is a potential substitute for biodiesel providing the country cheap and renewable source of energy for transport & power and can effect sizeable savings on foreign exchange.
- Jatropha oil has a very high saponification value and is being extensively used for soap making, lubricants and candles. The protein content in Jatropha oil cake may be used as a raw material for plastic and synthetic fibre.
- Jatropha plant has high medicinal value. The latex of Jatropha curcas contains an alkaloid known as Jatrophine, which is used in medicines.
- Jatropha oil cake is rich in nitrogen, phosphorous and potassium and can be used as organic manure.
- Revegetation of barren and denuded hills with Jatropha plants combats environmental pollution.
Thus, owing to its multiple uses, simple and cost effective technology, with or without irrigation makes it promising and profitable agro forestry crop ensuring optimum utilisation of land and manpower. It is a crop with low capital investment, short gestation period, long productive period and unlimited employment potential in rural areas.
Yield & Economics[edit | edit source]
The plant starts giving yield from the third year onwards and the benefits increase over the years and stabilizes in the 8th year. In the financial analysis with the above parameters of the investment cost & yields, the BCR & IRR works out to 1.19 & 19.41% respectively.