- Source: http://tim.cexx.org/?p=1282
Summary[edit | edit source]
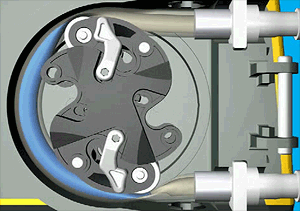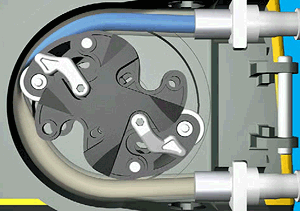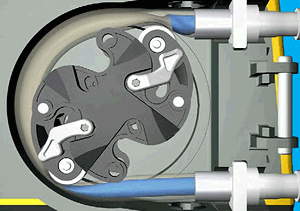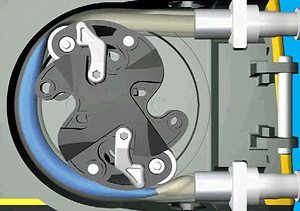
The pump prints as a single piece – no assembly required! – with captive rollers and no rotary bearing/wear surfaces. The only extra part needed is a length of surgical tubing to thread through the mechanism. This initial print is a proof-of-concept and is driven by a standard 1/4″(?) hex nut driver or Allen key: for a real application, you'd want to add a mount for an electric motor or similar.

OpenSCAD[edit | edit source]
// Planetary peristaltic pump (customizable)
// by Drmn4ea (drmn4ea at google's mail)
//
// Released under the Creative Commons - Attribution - Share Alike license ([https://creativecommons.org/licenses/by-sa/3.0/ http://creativecommons.org/licenses/by-sa/3.0/])
//
// Adapted from Emmett Lalish's Planetary Gear Bearing at [https://www.thingiverse.com/thing:53451 http://www.thingiverse.com/thing:53451]
// -------- Printer-related settings ------------
// Clearance to generate between non-connected parts. If the gears print 'stuck together' or are difficult to separate, try increasing this value. If there is excessive play between them, try lowering it. (default: 0.15mm)
tol=0.15;
// Allowed overhang for overhang removal; between 0 and 0.999 (0 = none, 0.5 = 45 degrees, 1 = infinite)
allowed_overhang = 0.75;
// -------- Details of the tubing used in the pump, in mm ------------
// Outer diameter of your tubing in mm
tubing_od = 4.7625;
// Wall thickness of your tubing
tubing_wall_thickness = 0.79375;
// Amount the tubing should be compressed by the rollers, as a proportion of total thickness (0 = no squish, 1.0 = complete squish)
tubing_squish_ratio = 0.5;
// -------- Part geometry settings ------------
// Approximate outer diameter of ring in mm
D=51.7;
// Thickness i.e. height in mm
T=15;
// Number of planet gears
number_of_planets=3;
// Number of teeth on planet gears
number_of_teeth_on_planets=7;
// Number of teeth on sun gear (approximate)
approximate_number_of_teeth_on_sun=9;
// pressure angle
P=45;//[30:60]
// number of teeth to twist across
nTwist=1;
// width of hexagonal hole
w=6.7;
DR=0.5*1;// maximum depth ratio of teeth
// ----------------End of customizable values -----------------
m=round(number_of_planets);
np=round(number_of_teeth_on_planets);
ns1=approximate_number_of_teeth_on_sun;
k1=round(2/m*(ns1+np));
k= k1*m%2!=0 ? k1+1 : k1;
ns=k*m/2-np;
echo(ns);
nr=ns+2*np;
pitchD=0.9*D/(1+min(PI/(2*nr*tan(P)),PI*DR/nr));
pitch=pitchD*PI/nr;
echo(pitch);
helix_angle=atan(2*nTwist*pitch/T);
echo(helix_angle);
phi=$t*360/m;
// compute some parameters related to the tubing
tubing_squished_width = tubing_od * (PI/2);
tubing_depth_clearance = 2*(tubing_wall_thickness*(1-tubing_squish_ratio));
// temporary variables for computing the outer radius of the outer ring gear teeth
// used to make the clearance for the peristaltic squeezer feature on the planets
outerring_pitch_radius = nr*pitch/(2*PI);
outerring_depth=pitch/(2*tan(P));
outerring_outer_radius = tol<0 ? outerring_pitch_radius+outerring_depth/2-tol : outerring_pitch_radius+outerring_depth/2;
// temporary variables for computing the outer radius of the planet gear teeth
// used to make the peristaltic squeezer feature on the planets
planet_pitch_radius = np*pitch/(2*PI);
planet_depth=pitch/(2*tan(P));
planet_outer_radius = tol<0 ? planet_pitch_radius+planet_depth/2-tol : planet_pitch_radius+planet_depth/2;
// temporary variables for computing the inside & outside radius of the sun gear teeth
// used to make clearance for planet squeezers
sun_pitch_radius = ns*pitch/(2*PI);
sun_base_radius = sun_pitch_radius*cos(P);
echo(sun_base_radius);
sun_depth=pitch/(2*tan(P));
sun_outer_radius = tol<0 ? sun_pitch_radius+sun_depth/2-tol : sun_pitch_radius+sun_depth/2;
sun_root_radius1 = sun_pitch_radius-sun_depth/2-tol/2;
sun_root_radius = (tol<0 && sun_root_radius1<sun_base_radius) ? sun_base_radius : sun_root_radius1;
sun_min_radius = max (sun_base_radius,sun_root_radius);
// debug raw gear shape for generating overhang removal
//translate([0,0,5])
//{
// //halftooth (pitch_angle=5,base_radius=1, min_radius=0.1, outer_radius=5, half_thick_angle=3);
// gear2D(number_of_teeth=number_of_teeth_on_planets, circular_pitch=pitch, pressure_angle=P, depth_ratio=DR, clearance=tol);
//}
translate([0,0,T/2])
{
// outer ring
difference()
{
// HACK: Add tubing depth clearance value to the total OD, otherwise the outer part may be too thin. FIXME: This is a quick n dirty way and makes the actual OD not match what the user entered...
cylinder(r=D/2 + tubing_depth_clearance,h=T,center=true,$fn=100);
exitholes(outerring_outer_radius-tubing_od/4,tubing_od, len=100);
union()
{
// HACK: On my printer, it seems to need extra clearance for the outside gear, trying double...
herringbone(nr,pitch,P,DR,-2*tol,helix_angle,T+0.2);
cylinder(r=outerring_outer_radius+tubing_depth_clearance,h=tubing_squished_width,center=true,$fn=100);
// overhang removal for top teeth of outer ring: create a frustum starting at the top surface of the "roller" cylinder
// (which will actually be cut out of the outer ring) and shrinking inward at the allowed overhang angle until it reaches the
// gear root diameter.
translate([0, 0, tubing_squished_width/2])
{
cylinder(r1=outerring_outer_radius+tubing_depth_clearance, r2=outerring_depth,h=abs(outerring_outer_radius+tubing_depth_clearance - outerring_depth)/tan(allowed_overhang*90),center=false,$fn=100);
}
}
}
// sun gear
rotate([0,0,(np+1)*180/ns+phi*(ns+np)*2/ns])
difference()
{
// the gear with band cut out of the middle
difference()
{
mirror([0,1,0])
herringbone(ns,pitch,P,DR,tol,helix_angle,T);
// center hole
cylinder(r=w/sqrt(3),h=T+1,center=true,$fn=6);
// gap for planet squeezer surface
difference()
{
cylinder(r=sun_outer_radius,h=tubing_squished_width,center=true,$fn=100);
cylinder(r=sun_min_radius-tol,h=tubing_squished_width,center=true,$fn=100);
}
}
// on the top part, cut an angle on the underside of the gear teeth to keep the overhang to a feasible amount
translate([0, 0, tubing_squished_width/2])
{
difference()
{
// in height, numeric constant sets the amount of allowed overhang after trim.
//h=abs((sun_min_radius-tol)-sun_outer_radius)*(1-allowed_overhang)
// h=tan(allowed_overhang*90)
cylinder(r=sun_outer_radius,h=abs((sun_min_radius-tol)-sun_outer_radius)/tan(allowed_overhang*90),center=false,$fn=100);
cylinder(r1=sun_min_radius-tol, r2=sun_outer_radius,h=abs((sun_min_radius-tol)-sun_outer_radius)/tan(allowed_overhang*90),center=false,$fn=100);
}
}
}
// planet gears
for(i=[1:m])
{
rotate([0,0,i*360/m+phi])
{
translate([pitchD/2*(ns+np)/nr,0,0])
{
rotate([0,0,i*ns/m*360/np-phi*(ns+np)/np-phi])
{
union()
{
herringbone(np,pitch,P,DR,tol,helix_angle,T);
// Add a roller cylinder in the center of the planet gears.
// But also constrain overhangs to a sane level, so this is kind of a mess...
intersection()
{
// the cylinder itself
cylinder(r=planet_outer_radius,h=tubing_squished_width-tol,center=true,$fn=100);
// Now deal with overhang on the underside of the planets' roller cylinders.
// create the outline of a gear where the herringbone meets the cylinder;
// make its angle match the twist at this point.
// Then difference this flat gear from a slightly larger cylinder, extrude it with an
// outward-growing angle, and cut the result from the cylinder.
planet_overhangfix(np, pitch, P, DR, tol, helix_angle, T, tubing_squished_width, allowed_overhang);
}
}
}
}
}
}
}
module planet_overhangfix(
number_of_teeth=15,
circular_pitch=10,
pressure_angle=28,
depth_ratio=1,
clearance=0,
helix_angle=0,
gear_thickness=5,
tubing_squished_width,
allowed_overhang)
{
height_from_bottom = (gear_thickness/2) - (tubing_squished_width/2);
pitch_radius = number_of_teeth*circular_pitch/(2*PI);
twist=tan(helix_angle)*height_from_bottom/pitch_radius*180/PI; // the total rotation angle at that point - should match that of the gear itself
translate([0,0, -tubing_squished_width/2]) // relative to center height, where this is used
{
// FIXME: This calculation is most likely wrong...
//rotate([0, 0, helix_angle * ((tubing_squished_width-(2*tol))/2)])
rotate([0, 0, twist])
{
// want to extrude to a height proportional to the distance between the root of the gear teeth
// and the outer edge of the cylinder
linear_extrude(height=tubing_squished_width-clearance,twist=0,slices=6, scale=1+(1/(1-allowed_overhang)))
{
gear2D(number_of_teeth=number_of_teeth, circular_pitch=circular_pitch, pressure_angle=pressure_angle, depth_ratio=depth_ratio, clearance=clearance);
}
}
}
}
module exitholes(distance_apart, hole_diameter)
{
translate([distance_apart, len/2, 0])
{
rotate([90, 0, 0])
{
cylinder(r=hole_diameter/2,h=len,center=true,$fn=100);
}
}
mirror([1,0,0])
{
translate([distance_apart, len/2, 0])
{
rotate([90, 0, 0])
{
cylinder(r=hole_diameter/2,h=len,center=true,$fn=100);
}
}
}
}
module rack(
number_of_teeth=15,
circular_pitch=10,
pressure_angle=28,
helix_angle=0,
clearance=0,
gear_thickness=5,
flat=false){
addendum=circular_pitch/(4*tan(pressure_angle));
flat_extrude(h=gear_thickness,flat=flat)translate([0,-clearance*cos(pressure_angle)/2])
union(){
translate([0,-0.5-addendum])square([number_of_teeth*circular_pitch,1],center=true);
for(i=[1:number_of_teeth])
translate([circular_pitch*(i-number_of_teeth/2-0.5),0])
polygon(points=[[-circular_pitch/2,-addendum],[circular_pitch/2,-addendum],[0,addendum]]);
}
}
//module monogram(h=1)
//linear_extrude(height=h,center=true)
//translate(-[3,2.5])union(){
// difference(){
// square([4,5]);
// translate([1,1])square([2,3]);
// }
// square([6,1]);
// translate([0,2])square([2,1]);
//}
module herringbone(
number_of_teeth=15,
circular_pitch=10,
pressure_angle=28,
depth_ratio=1,
clearance=0,
helix_angle=0,
gear_thickness=5){
union(){
//translate([0,0,10])
gear(number_of_teeth,
circular_pitch,
pressure_angle,
depth_ratio,
clearance,
helix_angle,
gear_thickness/2);
mirror([0,0,1])
gear(number_of_teeth,
circular_pitch,
pressure_angle,
depth_ratio,
clearance,
helix_angle,
gear_thickness/2);
}}
module gear (
number_of_teeth=15,
circular_pitch=10,
pressure_angle=28,
depth_ratio=1,
clearance=0,
helix_angle=0,
gear_thickness=5,
flat=false){
pitch_radius = number_of_teeth*circular_pitch/(2*PI);
twist=tan(helix_angle)*gear_thickness/pitch_radius*180/PI;
flat_extrude(h=gear_thickness,twist=twist,flat=flat)
gear2D (
number_of_teeth,
circular_pitch,
pressure_angle,
depth_ratio,
clearance);
}
module flat_extrude(h,twist,flat){
if(flat==false)
linear_extrude(height=h,twist=twist,slices=twist/6, scale=1)child(0);
else
child(0);
}
module gear2D (
number_of_teeth,
circular_pitch,
pressure_angle,
depth_ratio,
clearance){
pitch_radius = number_of_teeth*circular_pitch/(2*PI);
base_radius = pitch_radius*cos(pressure_angle);
depth=circular_pitch/(2*tan(pressure_angle));
outer_radius = clearance<0 ? pitch_radius+depth/2-clearance : pitch_radius+depth/2;
root_radius1 = pitch_radius-depth/2-clearance/2;
root_radius = (clearance<0 && root_radius1<base_radius) ? base_radius : root_radius1;
backlash_angle = clearance/(pitch_radius*cos(pressure_angle)) * 180 / PI;
half_thick_angle = 90/number_of_teeth - backlash_angle/2;
pitch_point = involute (base_radius, involute_intersect_angle (base_radius, pitch_radius));
pitch_angle = atan2 (pitch_point[1], pitch_point[0]);
min_radius = max (base_radius,root_radius);
intersection(){
rotate(90/number_of_teeth)
circle($fn=number_of_teeth*3,r=pitch_radius+depth_ratio*circular_pitch/2-clearance/2);
union(){
rotate(90/number_of_teeth)
circle($fn=number_of_teeth*2,r=max(root_radius,pitch_radius-depth_ratio*circular_pitch/2-clearance/2));
for (i = [1:number_of_teeth])rotate(i*360/number_of_teeth){
halftooth (
pitch_angle,
base_radius,
min_radius,
outer_radius,
half_thick_angle);
mirror([0,1])halftooth (
pitch_angle,
base_radius,
min_radius,
outer_radius,
half_thick_angle);
}
}
}}
module halftooth (
pitch_angle,
base_radius,
min_radius,
outer_radius,
half_thick_angle){
index=[0,1,2,3,4,5];
start_angle = max(involute_intersect_angle (base_radius, min_radius)-5,0);
stop_angle = involute_intersect_angle (base_radius, outer_radius);
angle=index*(stop_angle-start_angle)/index[len(index)-1];
p=[[0,0],
involute(base_radius,angle[0]+start_angle),
involute(base_radius,angle[1]+start_angle),
involute(base_radius,angle[2]+start_angle),
involute(base_radius,angle[3]+start_angle),
involute(base_radius,angle[4]+start_angle),
involute(base_radius,angle[5]+start_angle)];
difference(){
rotate(-pitch_angle-half_thick_angle)polygon(points=p);
square(2*outer_radius);
}}
// Mathematical Functions
//===============
// Finds the angle of the involute about the base radius at the given distance (radius) from it's center.
//source: http://www.mathhelpforum.com/math-help/geometry/136011-circle-involute-solving-y-any-given-x.html
function involute_intersect_angle (base_radius, radius) = sqrt (pow (radius/base_radius, 2) - 1) * 180 / PI;
// Calculate the involute position for a given base radius and involute angle.
function involute (base_radius, involute_angle) =
[
base_radius*(cos (involute_angle) + involute_angle*PI/180*sin (involute_angle)),
base_radius*(sin (involute_angle) - involute_angle*PI/180*cos (involute_angle))
];
