

The pulser pump is a simple, water powered mechanical device, also known as a bubble pump. Components of this pump have been used for various purposes, including the extraction of oil or in refrigeration cycles. Heat driven bubble pumps are most common, but this particular design of a pulser pump using the turbulent flow in a stream to trap air has yet to become common. The two main benefits of this pump are that it has no mechanical or moving parts, and that it doesn't use any chemicals, only the water from a stream. Once installed near a stream, the pump can lift water using only the energy from the stream.
I give permission to reuse and adapt any and all pictures and animated gifs that I have produced in the past for this project. Brian White, 3rd May 2010
Background Information[edit | edit source]
Overview[edit | edit source]
The pulser pump is a combination of a trompe and an air lift pump. Installed near a stream, the pulser pump can pump water to a height above the level of the stream. This allows streams in difficult-to-reach locations to be easily accessed, or water from a stream to be piped to a different location, for irrigation or drinking water purposes.
The pulser pump simply uses the trompe part to power the airlift part. A video explaining the pump can be seen here.
Benefits[edit | edit source]
As mentioned in the Introduction section, the main benefits of the pump are twofold. First, this design of pulser pump has no chemical components, as are common in heat-driven bubble pumps, which operate under similar principles (see Heat-Driven Bubble Pumps below). This allows the pump to be used for a large variety of tasks that require uncontaminated water to be pumped, such as irrigation and to pump drinking water. In addition, not requiring any chemicals, and using the stream water available as the pumping fluid greatly reduces the cost of the pump.
Secondly, the pulser pump has no moving components. Once installed, this pump uses the turbulent flow of the stream to trap air, and gravity to compress it (see Principle of Operation section below) to pump a portion of the water to a height above that of the stream. No mechanical components, which are typically more costly and more difficult to install, are required.
In addition to these benefits, it has also been claimed that pulser pumps have a positive effect on the quality of water by increasing the oxygen content.[1] The basic idea is that by mixing air and water together in the intake pump, the increased surface area between them allows more oxygen to be transmitted to the water than is typical in a stream. Further research should be done to confirm this idea.
History[edit | edit source]
Trompes were used before hydroelectric turbines to pump air into mines, to provide air for the pneumatic machines that made some of the first alpine tunnels and to provide air to drive motors that lit the wealthy parts of Paris in the late 19th century. Air lift pumps are still widely used by water utilities to pump water from very deep wells. They use compressors to push air down into the wells and the air erupts through a second wider pipe carrying water with it.
Principle of Operation[edit | edit source]
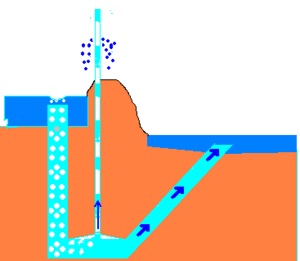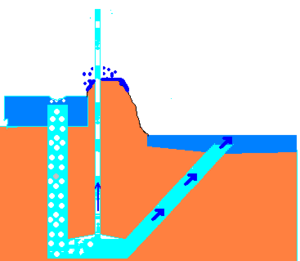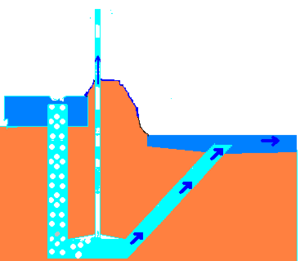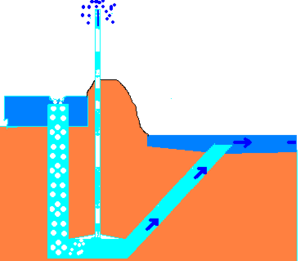
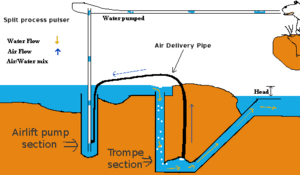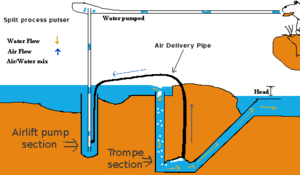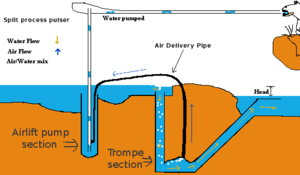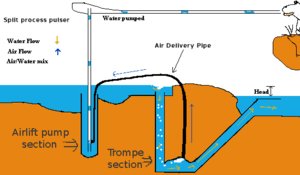

A pulser pump (aka bubble pump) uses a hydraulic head of water to compress air, which displaces water, pushing water "pulses" to a higher height than before. This works on the same principles as a trompe and an airlift pump.
Construction of a Model[edit | edit source]
Based on the success of other similar pilot projects,[2] a proof of concept model was constructed. The materials listed here are for the construction of a model, which can be used for small scale applications, such as those described in the Existing Pumps section below, or for further testing. The plastic tubing described here are flexible plastic tubing, which is useful for testing, as it can be bent to the correct height and reused for different tests, however solid PVC piping could also be used, and would be more practical to implement in a non-test situation. (See the Testing section.)
Materials[edit | edit source]
These materials are intrinsic components of this model pulser pump. Aside from scissors to cut the tubing, no additional tools were used.
-
Fig 1: 2 pieces of 3/4"Inner Diameter Clear Plastic Tubing
-
Fig 1a: 1 piece of 3/8"Inner Diameter Clear Plastic Tubing
-
Fig 1b: 2 @ 3/4"plastic tube connectors that fit inside the plastic tubing on one end and have threads on the other end
-
Fig 1c: 1 @ 3/8"compression fitting that fits around the tube on one end, compressing it into place, and has threads on the other end
-
Fig 1d: 1 @ 1 1/2" three way connector with two friction fit openings across from one another and one above
-
Fig 1e: 2 @ 1 1/2"to 3/4"connectors, threaded inside one end and friction fit on one end to connect to the three way connector and the plastic tube connector
-
Fig 1f: 1 @ 1 1/2"to 3/8"connector, threaded inside one end and friction fit on one end to connect to the three way connector and the plastic tube connector
In addition to the above items, these additional materials were required to setup this model and test it:
-
Fig 1: 1 hose to provide water in controlled manner
-
Fig 1a: supports and connection mechanisms to hold up tubing
-
Fig 1b: buckets and sink for draining excess water
Costs[edit | edit source]
The cost of this prototype were somewhat costly, however if compared to the costs of most other means of pumping water, it is very low. Additionally, if this design is constructed on a larger scale, it is likely that it could be built for a much lower cost. The costs of this prototype are approximated below:
| Item | Price |
| Plastic Tubing | $40 |
| Tubing Connectors (all) | $10 |
| Three Way Connector | $10 |
| Total | $60 |
Building and Setting Up the Model[edit | edit source]
The process is very straight-forward to build this model, as it has very few components. The tricky part comes with setting up the tubes so they stay as vertical as possible.
A video of the model I made, when working, is shown below. Note the bubbles in the tubes that clearly demonstrate that the inlet tube is in the Bubble Flow Regime, and the pumping tube is in Slug Flow.
The process used to build this model is described in detail below.
- First, the tubes must be cut to the desired length.
- In this model, the inlet 3/4" tube was cut to be approximately 2.1m long.
- The outlet tube was also cut to be 2.1m long, so it could be varied to perform different tests
- The pumping tube was kept long in order to be able to vary the height in the tests described below.
- In this model, the three way connector is used as the separation container for the pulser pump.
- The 1 1/2"to 3/4"connectors were fit snugly into the directly opposing sides of the three way connector. Epoxy can be applied to ensure a tightly sealed fit.
- The 1 1/2"to 3/8"connector was fit into the three way connector hole that is 90 degrees from either of the other two holes.
- First, screw in the compression fitting for the 3/8" connection to the 1 1/2"to 3/8"connector
- Then, screw in the plastic tube fittings for the 3/4" connection to the 1 1/2"to 3/4"connectors
- By connecting these before connecting the tubing, the tubing won't become tangled.
- The 3/4" tubing should fit tightly over the 3/4" connector. It can be further held in place by tightening a metal clamp around it.
- The 3/8" compression has a component that goes around the outside of the tubing, a small piece fits inside the tubing to hold it open, then the piece that is around the outside of the tubing can be screwed into the compression fitting already connected to the 1 1/2"to 3/8"connector, holding the tube in place.
- Now all the main components of the pump are connected. The next stage is to set up the pump.
- First, determine a method of holding the tubes in place. For this, a wooden backboard can be used and the tubes can be nailed to it. In order to have an easily adjustable device, in this experiment the tubes were attached with tape to the support system and wall.
- Make sure the tubes are vertical, and that the heights of the tubes are as desired.
- A hose was connected to the top of the inlet tube by inserting both the 3/4" diameter tube and the hose nozzle into a short 1" diameter scrap tube. The hose was used to simulate the flow of the stream.
- The outlet tube was set to drain into the sink.
Testing[edit | edit source]
After setting up the model, a few preliminary tests were run to show that the pump can indeed produce useful work. Much more detailed testing is required before this design of a pulser pump will gain more widespread acceptance and use.
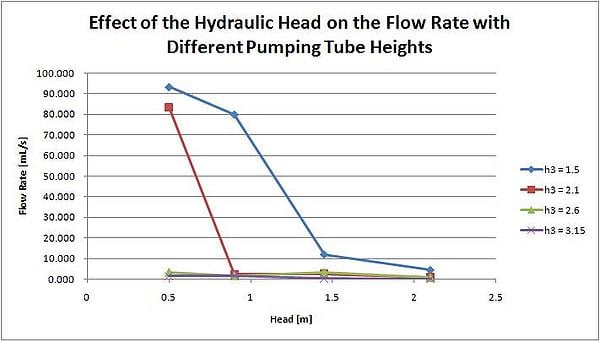
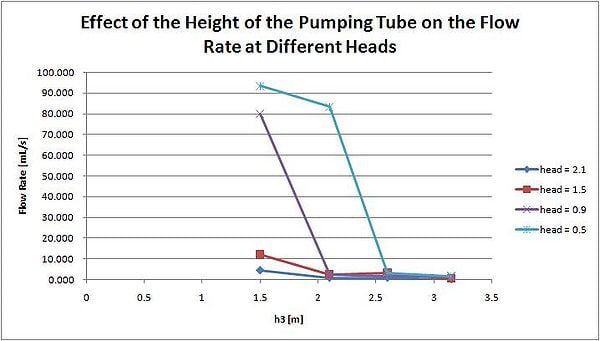
In this test, two variables were changed, the hydraulic head on the pump, and the height of the pumping tube.
It is expected that as the hydraulic head increases, the flow rate will also increase. This effect was demonstrated by the pump, and the results are shown below.
As the height of the pumping tube increases, more energy is required for the pulses to reach the top of the tube. The corresponding decrease in flow rate expected can be seen below.
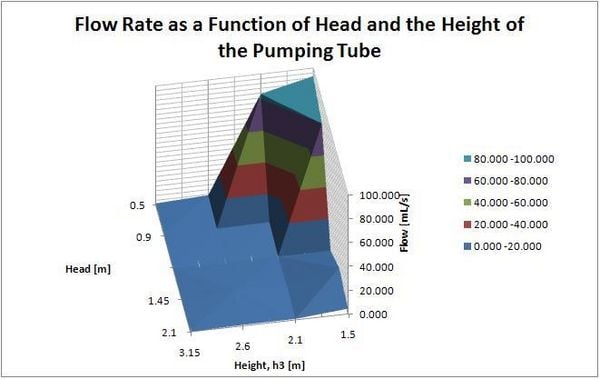
When the effects of both these variables are combined, the result is a plot showing how the flow rate depends on both hydraulic head and the height of the pumping tube. This plot can be used to demonstrate the relationship between both these quantities and flow rate. Even at large hydraulic heads, the flow rate could be small if the height of the pumping tube is large. Additionally, even when the height of the pumping tube is small, a small head will reduce the amount of water pumped through the pumping tube. This is shown below.
At peak performance (large head and short pumping tube), this model pumped at a rate reaching nearly 100mL/s, or 1L every 10 seconds! Despite multiple tests at each value, the reproducibility of these results is still questionable. Regardless of the exact rate of flow, this experiment shows that there is a huge potential for the pulser pump to be widely used to pump water. Further testing should be done to better evaluate the exact relationship between flow, head and the height of the pumping tube.
Scientific Model[edit | edit source]
Despite the fact that pulser pumps, or at least various similar designs of this sort of pump, have existed for a fairly long time, there is not a good explanation or model that describes them. Similar problems, such as for Heat-Driven Bubble Pumps, often are closed systems, which don't require an outlet pipe. In this section, some of the scientific principles behind how this pump functions are presented, and two different models are developed. The first model is the simple Manometer Model, and the second is the more complicated Pressure Model.
Two Phase Flow[edit | edit source]
An important concept for this design is two phase flow, which is when there is a liquid and a gas separated by a meniscus. There are at least seven different regimes of two phase flow,[3] several of which are exhibited during the operation of the pulser pump.
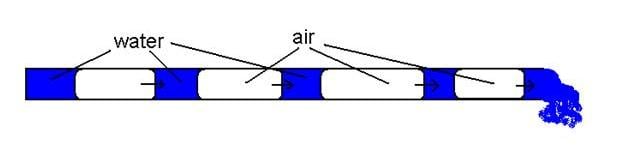
Slug Flow[edit | edit source]
The lifting action of the pump up the pumping tube occurs mostly in the slug flow regime. In slug flow, the liquid and gas separate into different layers occupying nearly the entire cross section of the tube, as shown below.
For flow in the slug regime, the diameter of the tube allowed depends on the speed of the flow and its viscosity. The velocity in the pump tube is very difficult to describe, even with several simplifying assumptions. For example, if the tube is not vertical, the bubbles are no longer symmetric resulting in changes in the speed of the bubbles. Several dimensionless terms including the Froude number, the Eotvos number and the Reynolds number are required to fully describe the flow.[4] Although there is still not clear agreement on the most appropriate model, several have been proposed.[5]
The full determination of the fluid properties during slug flow and derivation of a model including the full effects of this flow regime are beyond the scope of this model. Instead, a much simpler model is considered, assuming completely vertical tubes and steady flow, etc. as discussed further below.
Manometer Model[edit | edit source]

With multiple tubes in the same liquid, the maximum height of the liquid in each tube is given by conservation of mass. Using the same principle as a manometer, the external pressure, density, and diameter of the tube determine the height of the liquid. This means that the density, ρ, times the cross sectional area of the tube, A, times the height of the fluid, h, is the same for each tube when they exit to the same pressure, as shown in the diagram to the right. This means that if a closed container is full of water with two of the same straws at the top that are open to the air, the liquid in the straws will rise to the same height, i.e. there will not be more liquid in one straw than the other.
That is to say:
This makes sense if all the variables are constant. In a pulser pump, the problem is more complicated. There is an inlet tube and an outlet tube, with the same cross section, but different heights, and then there is the pumping tube with a smaller area and higher height. The inlet and outlet tubes are almost completely filled with water, and so the density can be approximated as that of water, however, at a given time, the pumping tube has a large portion of the tube full of air, not water. The above equation then becomes:
Or, if the inlet and outlet pipes have the same cross sectional area:
Where is the hydraulic head. The height that the water can be pumped to can then be determined by solving for
The main problem with this model is that it ignores the velocity of the fluid as it travels through the pump. This is a non-negligible quantity, as if the motion of the fluid was negligible, the air in the outlet tube would separate from the water, and the pump would lose its ability to move water. This manometer model does illustrate the basic principle of the pump, however, and disproves the most common criticism for the pulser pump, which is that it is physically impossible for the smaller pumping tube to pump water above the initial height of the stream. The above argument shows that this is only true if the fluid in the pumping tube is stationary, or if the amount of air present is negligible.
Pressure Model[edit | edit source]
Theory[edit | edit source]

To account for the velocity, the flow needs to be evaluated in greater detail, using conservation of energy and Bernoulli's Equation. This method models the change in pressure of the flow at the different points
At location 4, the pressure from location 1 is given by:
Similarly, at 5 from 2:
And at 6 from 3:
The velocity at 3 is assumed to be zero, in order to determine the maximum height that the water can be pumped to. This will provide an upper limit on the height the water can reach. Also, the pressures at 1, 2, and 3 can be assumed to be approximately one atmosphere, as '3' exits to the atmosphere and '1' and '2' only have a very small hydrostatic pressure, associated with the depth of the stream. Performing a control volume analysis on the bottom container between 4, 5, and 6, conservation of mass dictates:
The areas of all the tubes are known from the geometry of the experiment. The outlet tube has minimal air content, so the density can be assumed to equal that of water.
Building on the work of one source,[6] which analysed a heat-driven bubble pump in a closed system, the change in pressure from 4 and 5 to 6 can be described as follows:
Up to this point in the derivation, all the assumptions have been for a fairly general case. The following assumptions in the model provide a more specific, simplified model. The first assumption is that the velocity between 4 and 5 is approximately constant. As only a small portion of the fluid is diverted to exit out the pumping tube, it is assumed the majority of the fluid maintains its momentum while continuing though the outlet tube.
Secondly, the gas content in the slug regime within the pumping tube is assumed to be 70%, which is an average value for slug flow. Also, the gas in the inlet tube is assumed to be in the bubble flow regime, where the gas content is on average 30%.[7] These mean that:
Testing the Theory[edit | edit source]

With these seven equations, and accompanying assumptions, the Pressure Model still has one more unknown than equation, which means that a reasonable height must be determined through iteration. The inputs are the geometric parameters of the system, and the pressure and velocity at '4' where the highest pressure is expected to occur, should be output. If these values are reasonable, the system can be set up to function; if not, then another iteration should occur.
A first pass at modeling this system was done using EES software. The above equations were defined, and some initial conditions were set. As can be seen in the image, the height and diameters of the tubes and the velocity of the stream at 1 and 2 must be entered, in addition to the assumptions listed above. The program then outputs the velocity throughout the tube, and the pressures. In order to better assess the validity of this model, this EES program or a similar one can be used.
Existing Pulser Pumps[edit | edit source]
Pulser pumps lack credibility because there has been no peer review, although they are starting to be researched further (see the External Links below). Several models have been built however, and videos are available online to show how they work, and them working. This design of pulser pump is not patented, and the designs are in the public domain.[8]
Working Pulser Pump[edit | edit source]
An example of a 20 year old working pulser pump is available here, if it does not load below. This pump is powered by a little stream with 300 litres of water falling 0.5 meters producing the power. Figures from that pump show that an apparent water speed down the tromp part of between 0.32 meters per second and 0.68 meters per second is fast enough to send the air bubbles down the pipe.
The apparent air speed up the airlift section seems to work best between 0.7 ms-1 and and 1.5 meters per second. This was when using 12 mm and 19 mm pipes and pumping straight up.
A lower apparent air speed worked best when pumping up an incline. (Apparent speed is the speed of the water or air through the pipes assuming that only one fluid was in the pipe) It is a good guide if you make your own. Brian
Pulser pumps can work with much larger flows and heads than that according to Gaiatechnician.
Because of their extreme simplicity, they can be of great value to waterside communities. The tiny pulser pump in the video can pump about 5 tonnes of water per day to a storage container.[9]
A second example (shown here) uses the pulser pump to provide water for animals. It has a supply flow rate of approximately 30 litres/min through a 40mm waste pipe. It can lift 30 mL/min to 3m or 1 L/min to 1m.[10]


Mike Donevan of practical farm ideas has allowed me to use pictures and text from when the pump was in his magazine in exchange for a link. http://www.farmideas.co.uk/
I think they will be valuable to anyone who wants ball park figures to guess at good pipe sizes for their projects
Brian white
Heat-Driven Bubble Pumps[edit | edit source]

Heat-Driven Bubble pumps are the most common type of pulser pump found. They use a similar principle of operation as this pulser pump design, but in a closed system. In general, a refrigerant with a boiling point below that of water is mixed with the fluid. After the mixture is compressed, it is heated causing bubbles to form from the refrigerant in the working fluid. The bubbles of refrigerant then push the water up the pump tube, as in the pulser pump. The mixture then enters a separation chamber, where the liquid is sent to an absorber and the refrigerant to a condenser.[11]
Conclusions[edit | edit source]
This particular design for a pulser pump is extremely simple to build, and has the potential to make a large impact in how water is pumped. It does not use chemicals to pump the water, so the water let back into the stream is not contaminated. On the contrary, claims have been made that indicate the water returned to the stream contains more oxygen, providing a better environment for underwater creatures. The water that is not returned to the stream can be used to irrigate land or provide drinking water. The added elevation that the pump provides allows water to be transported further than the stream alone would be able to move it.
The pump itself is made of very few materials, only simple tubes and connections, and after optimum design is found, it could be made inexpensively. Almost no maintenance is required once the pump is set up, so aside from the initial installation and equipment costs, the pump can provide water cheaply and easily to those nearby.
In this analysis, both an experimental model and a theoretical model were developed. The experimental model was based off a previous design, and acted as a proof of concept. The model clearly indicated the trends expected, showing highest flow rates for a large hydraulic head and a short pumping tube. Two theoretical models were proposed, the first based on the principle of conservation of mass, like a manometer. This model provided a rough estimate for the height of the second tube, but the validity is very limited because it assumes a negligible velocity, however it does serve to disprove the idea that this design for a pulser pump is physically impossible. The second theoretical model used both conservation of mass and conservation of energy to evaluate the velocities and pressures at each stage of the pump. This second model requires the user to iterate on the values produced in order to determine a reasonable geometry under specific conditions. Using Engineering Equation Solver, a template was formed that would allow the user to iterate on the assumptions made in order to determine the optimum geometry.
Recommendations[edit | edit source]
Both the experimental and the theoretical model would benefit greatly from a peer review and further research. The experimental model should be tested using a more rigid testing scheme, with many more tests at each height and head. Other variables such as the size of the container, the diameter of the tubes and the flow velocity should also be tested to determine their effects on the pulser pump, and a wider range of values should be used. The main setback encountered during this experiment was leakage though the original container and hose. By using the methods described above, these problems can easily be overcome and more time can be spent performing more detailed tests.
The theoretical model proposed could be further expanded and tested using software such as the EES program described above. In addition, there are several factors that were not accounted for that must be included in the model for it to accurately predict the flow rate through the pump. These include:
- Analysis of two phase slug flow in pumping tube
- Determination of air content and flow regime in inlet and outlet tubes
- Friction/Viscous losses
- Turbulent Flow
- Pressure gradient across separation container
External links[edit | edit source]
- Gaiatechnician's explaination on YouTube can be found here. For a more detailed explaination, visit his website
- Other videos of working pulser pumps can be found here and here
- Bubble Action Pumps Ltd. make a similar product, that pumps water through solar thermal panels. Check it out on their website.
- Altenergymag describes pulser pumps here
- All About Pumps also have a description here
- For a description of how to make a pulser pump, visit Instructables
References[edit | edit source]
- ↑ All About Pumps. Available at: http://web.archive.org/web/20210125002710/http://www.animatedsoftware.com/pumpglos/glpulser.htm [Accessed April 15, 2010].
- ↑ Brian White "Pulser Pumps" Available Online: http://nxtwave.tripod.com/gaiatech/pulser/builder.htm [Accessed April 3, 2010]
- ↑ J. B. McQuillen, R. Vernon and A. E. Dukler. "Flow regimes in gas-liquid flows" Available Online at: http://web.archive.org/web/20170704025739/http://www3.nd.edu/~mjm/flow.regimes.html [Accessed April 15, 2010]
- ↑ J. Fabre and A. Line "Modeling of Two-Phase Slug Flow" Annu. Rev. Fluid Mech: 1992. Available Online: http://arjournals.annualreviews.org/doi/pdf/10.1146/annurev.fl.24.010192.000321?cookieSet=1 [Accessed April 15, 2009]
- ↑ XIA Guo-dong, CUI Zhen-zhen, LIU Qing, ZHOU Fang-de, HU Ming-sheng "A Model for Liquid Slug Length Distribution in Vertical Gas-Liquid Slug Flow" Journal of Hydrodynamics: 2009. Available Online: [Accessed April 15, 2010]
- ↑ Susan J. White. "Bubble Pump Design and Performance" Georgia Institute of Technology: August 2001. Available Online at: http://www.me.gatech.edu/energy/SusanThesis.pdf [Accessed April 13, 2010].
- ↑ Micro Motion White Paper. "Explaining how two-phase flow affects mass flowmeters" Micro Motion, Inc. USA: 2004. Available online: http://web.archive.org/web/20130123193851/http://www.documentation.emersonprocess.com:80/groups/public_public_mmisami/documents/whitepaper/wp-00698.pdf [Accessed: April 15, 2010]
- ↑ Brian White "The Pulser Pump." Available at: http://www.altenergymag.com/emagazine.php?issue_number=03.10.01&article=pulser [Accessed April 15, 2010].
- ↑ Pulser Pump (Air Lift Pump). Available at: http://ca.youtube.com/watch?v=oxJTC77PADQ [Accessed April 15, 2010].
- ↑ cornish pulser pump. Available at: http://www.youtube.com/watch?v=Tf1-7fL_UIk [Accessed April 15, 2010].
- ↑ Susan J. White. "Bubble Pump Design and Performance" Georgia Institute of Technology: August 2001. Available Online at: http://www.me.gatech.edu/energy/SusanThesis.pdf [Accessed April 13, 2010].

















_{pump}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/186fa09ca298967fbea8a409ab958aa6a1024310)
_{pump}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d95dbd316e21fe0d91aced359f606e1cbd0bca2e)


![{\displaystyle h_{pump}={\frac {\rho _{water}A(h_{inlet}-h_{outlet})}{[\rho _{water}\%_{water}+\rho _{air}\%_{air}]A_{pump}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5130c96622af52a244433b6f4885a78aa475a126)







